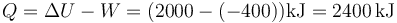Proceso con presión proporcional a volumen
De Laplace
(→Enunciado) |
(→Trabajo sobre el gas) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 5: | Línea 5: | ||
# Calcule el trabajo realizado sobre el gas en este proceso. | # Calcule el trabajo realizado sobre el gas en este proceso. | ||
# Determine la variación de la energía interna del gas y el calor que entra en él en el proceso. | # Determine la variación de la energía interna del gas y el calor que entra en él en el proceso. | ||
| + | |||
| + | ==Temperatura final== | ||
| + | La temperatura final la obtenemos de la ley de los gases ideales | ||
| + | |||
| + | <center><math>\frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad T_B=T_A\frac{p_B}{p_A}\frac{V_B}{V_A}</math></center> | ||
| + | |||
| + | Al ser la presión proporcional al volumen, si cuando el volumen es 1 m³ la presión es de 100 kPa, cuando el volumen es 3 m³ la presión será 300 kPa. | ||
| + | |||
| + | Por tanto la temperatura final es | ||
| + | |||
| + | <center><math>T_B = 300\,\mathrm{K}\frac{300}{100}\,\frac{3}{1}=2700\,\mathrm{K}</math></center> | ||
| + | |||
| + | ==Trabajo sobre el gas== | ||
| + | Al ser el proceso cuasiestático, podemos hallar el trabajo a partir de la gráfica en un diagrama pV. | ||
| + | |||
| + | Por ser la presión proporcional al volumen, el proceso es un segmento rectilíneo. El área bajo este segmento es la de un trapecio. El trabajo es igual a esta área cambiada de signo | ||
| + | |||
| + | <center><math>W=-\left(\frac{p_A+p_B}{2}\right)(V_B-V_A) = -\frac{100+300}{2}\times 2\,\mathrm{kJ}=-400\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | <center>[[Archivo:trabajo-segmento.png|400px]]</center> | ||
| + | |||
| + | Este trabajo también puede hallarse a partir de la integral de la presión | ||
| + | |||
| + | <center><math>W=-\int_{V_A}^{V_B}p\,\mathrm{d}V</math></center> | ||
| + | |||
| + | ==Energía interna y calor== | ||
| + | ===Variación en la energía interna=== | ||
| + | La energía interna es una función de estado, por lo que podemos hallar su incremento restando el valor inicial del final | ||
| + | |||
| + | <center><math>\Delta U = \frac{p_BV_B-p_AV_A}{\gamma-1}=\frac{5}{2}(300\times 3-100\times 1)\mathrm{kJ}=2000\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ===Calor que entra en el gas=== | ||
| + | Una vez que tenemos el trabajo y la variación de la energía interna, calculamos el calor que entra a partir del primer principio de la termodinámica | ||
| + | |||
| + | <center><math>Q=\Delta U - W = (2000-(-400))\mathrm{kJ}=2400\,\mathrm{kJ}</math></center> | ||
[[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | [[Categoría:Problemas del primer principio de la termodinámica (GIE)]] | ||
última version al 16:28 4 abr 2016
Contenido |
1 Enunciado
Se tiene un volumen de 1 m³ de un gas ideal diatómico (γ = 1.4), a 100 kPa y 300 K. Sobre este gas se realiza un proceso cuasiestático en el que se aumenta gradualmente su presión y volumen de forma que en todo momento su presión es proporcional al volumen ocupado, p = λV. Al final del proceso, el volumen del gas es de 3 m³.
- Halle la temperatura final del gas.
- Calcule el trabajo realizado sobre el gas en este proceso.
- Determine la variación de la energía interna del gas y el calor que entra en él en el proceso.
2 Temperatura final
La temperatura final la obtenemos de la ley de los gases ideales

Al ser la presión proporcional al volumen, si cuando el volumen es 1 m³ la presión es de 100 kPa, cuando el volumen es 3 m³ la presión será 300 kPa.
Por tanto la temperatura final es
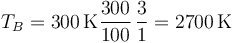
3 Trabajo sobre el gas
Al ser el proceso cuasiestático, podemos hallar el trabajo a partir de la gráfica en un diagrama pV.
Por ser la presión proporcional al volumen, el proceso es un segmento rectilíneo. El área bajo este segmento es la de un trapecio. El trabajo es igual a esta área cambiada de signo
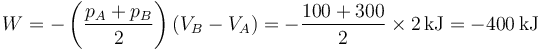

Este trabajo también puede hallarse a partir de la integral de la presión
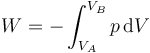
4 Energía interna y calor
4.1 Variación en la energía interna
La energía interna es una función de estado, por lo que podemos hallar su incremento restando el valor inicial del final

4.2 Calor que entra en el gas
Una vez que tenemos el trabajo y la variación de la energía interna, calculamos el calor que entra a partir del primer principio de la termodinámica