Entrar Página Discusión Historial Go to the site toolbox

Cuatro planos y fuente de tensión

De Laplace

(Diferencias entre revisiones)
(→Cargas y potenciales)
(→Estado tras la conexión)
Línea 115: Línea 115:
===Estado tras la conexión===
===Estado tras la conexión===
 +
Cuando el interruptor pasa de la posición A a la B, la placa 3 pasa de estar aislada y descargada a estar conectada a una fuente que fija su tensión en <math>V_0</math> (y su carga pasa a ser desconocida).
 +
 +
Parecería entonces que este apartado es i´dentico al anterior, cambiando la placa 2 por la 3 y viceversa, pero no es así. La diferencia con el caso anterior es que ahora la placa 2 está cargada. Cuando se desconecta la fuente, la placa no se descarga mágicamente. El proceso de desconexión lo que implica es que a partir de ese momento la carga de la placa permanece constante. Su valor será el que tenía en ese momento, que es que el que calculamos en el apartado anterior.
 +
 +
Por tanto, nuestros datos son ahora
 +
 +
<center><math>Q_2 = \frac{3C_0V_0}{2}</math>{{qquad}}<math>V_3=V_0\,</math></center>
 +
 +
y el sistema de ecuaciones resultante
 +
<center>
 +
<math>\frac{3C_0V_0}{2}=C_0\left(2V_2-V_0\right)</math>{{qquad}} <math>Q_3 = C_0\left(-V_2+2V_0\right)</math></center>
 +
tiene por solución
 +
 +
<center><math>V_2 = \frac{5}{4}V_0</math>{{qquad}} <math>Q_3 = \frac{3C_0V_0}{4}</math>
 +
</center>
 +
 +
Obsérvese que el potencial de la placa 2 no solo no va a 0 por efecto de la desconexión, sino que incluso aumenta.
 +
 +
El cálculo de las restantes cargas es inmediato
 +
 +
<center><math>Q_1 = C_0(0-V_2) = -\frac{5C_0V_0}{4}</math>{{qquad}}<math>Q_4 = C_0(V_4-V_3) = -C_0V_0</math></center>
 +
===Carga transferida y trabajo===
===Carga transferida y trabajo===
[[Categoría:Problemas de campo eléctrico en presencia de conductores]]
[[Categoría:Problemas de campo eléctrico en presencia de conductores]]

Revisión de 17:14 15 ene 2009

Contenido

1 Enunciado

Se tiene un sistema formado por cuatro placas cuadradas de lado L, situadas paralelamente a una distancia a cada una de la siguiente. Entre las placas hay vacío.

Las dos placas exteriores (“1” y “4”) se encuentran permanentemente a tierra.

  1. Inicialmente, la placa 2 se encuentra conectada a un generador e tensión V0 mientras que la 3 está aislada y descargada. Calcule el campo eléctrico en cada una de las tres regiones, la carga y el voltaje de las cuatro placas en este estado, así como la energía electrostática almacenada en el sistema.
  2. De forma abrupta, sin dar tiempo a que las placas se descarguen, el interruptor se pasa de la posición A la B, pasando la fuente a estar conectada a la placa 3. Halle los nuevos valores de los campos, las cargas, las tensiones y la energía almacenada una vez que se ha alcanzado de nuevo el equilibrio electrostático.
  3. Suponga que a la salida de la fuente de tensión se coloca un amperímetro y un integrador, de forma que se puede saber la carga que pasa por el cable durante el periodo transitorio. ¿Qué valor dará esta lectura? ¿Qué trabajo realiza la fuente durante este periodo transitorio?

2 Solución

2.1 Cargas, campos y potenciales

2.1.1 Cargas y potenciales

Aunque el sistema está formado por cuatro placas, puede considerarse como formado por solo dos conductores, ya que las placas exteriores, que se encuentran permanentemente a tierra, funcionan simplemente como referencia, actuando como 6ldquo;el infinito” en un sistema arbitrario de conductores. Los únicos conductores “vivos”, en el sentido de que podemos variar sus potenciales o fijar sus cargas, son las dos placas centrales.

Considerado como un sistema de dos conductores, el circuito equivalente estará formado por tres condensadores, que en este caso son de placas planas y paralelas. Puesto que la sección y la distancia entre placas son las mismas en todos los casos, las capacidades son todas iguales

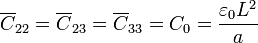
\overline{C}_{22}=\overline{C}_{23}=\overline{C}_{33}=C_0 = \frac{\varepsilon_0 L^2}{a}

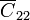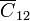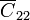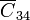Aquí \overline{C}_{22} representa la capacidad que forma el conductor 2 con tierra, que en este caso es el conductor 1. Por ello, sería equivalente que pusiéramos \overline{C}_{12} o \overline{C}_{22} en este caso; lo mismo con \overline{C}_{33} y \overline{C}_{34}.

Esto nos da los coeficientes de capacidad

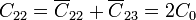
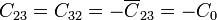
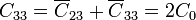
C_{22} = \overline{C}_{22}+\overline{C}_{23} = 2C_0    C_{23}=C_{32}=-\overline{C}_{23} = -C_0    C_{33} = \overline{C}_{23}+\overline{C}_{33} = 2C_0

o, en forma matricial

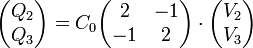
\begin{pmatrix}Q_2\\ Q_3 \end{pmatrix}=C_0\begin{pmatrix}2 & -1 \\ -1 & 2\end{pmatrix}\cdot\begin{pmatrix}V_2\\ V_3\end{pmatrix}

Lo que conocemos en este primer apartado es que

V2 = V0    Q3 = 0

lo que nos da el sistema de ecuaciones

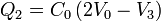
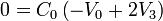
Q_2 = C_0\left(2V_0-V_3\right)    0 = C_0\left(-V_0+2V_3\right)

con solución

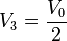
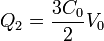
V_3 = \frac{V_0}{2}    Q_2 = \frac{3C_0}{2}V_0

Las cargas de las placas exteriores las obtenemos considerando los condensadores que forman con las placas 2 y 3. Nos da

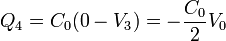
Q1 = C0(0 − V2) = − C0V0     Q_4 = C_0(0-V_3) = -\frac{C_0}{2}V_0

El sistema es globalmente neutro, como corresponde a que no haya campo en el exterior del sistema

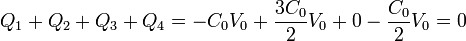
Q_1+Q_2+Q_3+Q_4 = -C_0V_0+\frac{3C_0}{2}V_0+0-\frac{C_0}{2}V_0 = 0

2.1.2 Empleando el circuito equivalente

Las cargas y tensiones se pueden calcular usando exclusivamente el circuito equivalente. Tenemos por cada uno de las dos placas centrales, los tres condensadores del sistema, y una fuente de tensión conectada al nodo 2. Puesto que la placa 3 se encuentra aislada y descargada no es preciso incluir ninguna fuente adicional.

Para hallar la carga en la placa 2, simplemente observamos que se encuentra conectada a tierra por dos ramas, una con un solo condensador C0 y otra formada por dos condensadores C0 puestos en serie. La capacidad equivalente de la asociación será

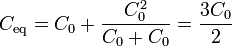
C_\mathrm{eq}=C_0+\frac{C_0^2}{C_0+C_0} = \frac{3C_0}{2}

y por tanto la carga del nodo 2 es

Q_2 = C_\mathrm{eq}V_0 = \frac{3C_0}{2}V_0

Esta carga se distribuye entre las dos ramas, atendiendo a su capacidad. Para el condensador que la placa 2 forma con la 1

Q2a = C0V0

y por tanto, en la placa 1, que es la negativa de este condensador

Q1 = − C0V0

la carga en la segunda rama, formada por los dos condensadores (cuya asociación teien capacidad C0 / 2) es

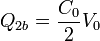
Q_{2b}=\frac{C_0}{2}V_0

El potencial del conductor 3 lo sacamos de que conocemos la carga del condensador C0 que forma con tierra. Esta carga es la que acabamos de calcular. Por tanto

V_3 = \frac{Q_{2b}}{C_0} = \frac{V_0}{2}

Este resultado es evidente simplemente observando que la caída de potencial en los dos condensadores debe ser la misma (pues son iguales) y por tanto en cada uno de ellos cae la mitad del total.

La carga de la placa 4 es la de la placa negativa del condensador que forma con la 3

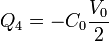
Q_4 = -C_0\frac{V_0}{2}

2.1.3 Campo eléctrico

Para hallar el campo eléctrico no nos basta el circuito equivalente, ya que necesitamos saber qué ocurre dentro de los condensadores. No obstante, el campo en un condensador plano es extremadamente sencillo:

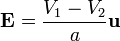
\mathbf{E}=\frac{V_1-V_2}{a}\mathbf{u}

siendo 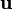\mathbf{u} el vector unitario que va de la placa 1 a la 2.

Aplicando esto a cada uno de los tres condensadores resulta

  • Entre la placa 1 y la 2
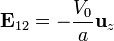
\mathbf{E}_{12}=-\frac{V_0}{a}\mathbf{u}_z
  • Entre la 2 y la 3
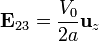
\mathbf{E}_{23}=\frac{V_0}{2a}\mathbf{u}_z
  • Entre la 3 y la 4
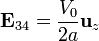
\mathbf{E}_{34}=\frac{V_0}{2a}\mathbf{u}_z

siendo \mathbf{u}_z el vector que va de la placa 1 a la 4.

2.1.4 Energía almacenada

La energía electrostática del sistema de dos conductores 2 y 3 es

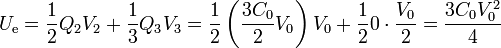
U_\mathrm{e}=\frac{1}{2}Q_2V_2+\frac{1}{3}Q_3V_3 = \frac{1}{2}\left(\frac{3C_0}{2}V_0\right)V_0+\frac{1}{2}0\cdot \frac{V_0}{2} = \frac{3C_0V_0^2}{4}

Nótese que es indiferente incluir las placas 1 y 4, pues al ser su potencial nulo no contribuyen al sumatorio.

En términos del circuito equivalente, el sistema se reduce a un solo condensador

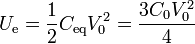
U_\mathrm{e}=\frac{1}{2}C_\mathrm{eq}V_0^2 = \frac{3C_0V_0^2}{4}

2.2 Estado tras la conexión

Cuando el interruptor pasa de la posición A a la B, la placa 3 pasa de estar aislada y descargada a estar conectada a una fuente que fija su tensión en V0 (y su carga pasa a ser desconocida).

Parecería entonces que este apartado es i´dentico al anterior, cambiando la placa 2 por la 3 y viceversa, pero no es así. La diferencia con el caso anterior es que ahora la placa 2 está cargada. Cuando se desconecta la fuente, la placa no se descarga mágicamente. El proceso de desconexión lo que implica es que a partir de ese momento la carga de la placa permanece constante. Su valor será el que tenía en ese momento, que es que el que calculamos en el apartado anterior.

Por tanto, nuestros datos son ahora

Q_2 = \frac{3C_0V_0}{2}    V_3=V_0\,

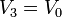
y el sistema de ecuaciones resultante

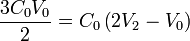
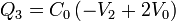
\frac{3C_0V_0}{2}=C_0\left(2V_2-V_0\right)     Q_3 = C_0\left(-V_2+2V_0\right)

tiene por solución

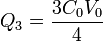
V_2 = \frac{5}{4}V_0     Q_3 = \frac{3C_0V_0}{4}

Obsérvese que el potencial de la placa 2 no solo no va a 0 por efecto de la desconexión, sino que incluso aumenta.

El cálculo de las restantes cargas es inmediato

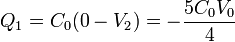Q_1 = C_0(0-V_2) = -\frac{5C_0V_0}{4}    Q4 = C0(V4 − V3) = − C0V0

2.3 Carga transferida y trabajo

Obtenido de "http://tesla.us.es/wiki/index.php/Cuatro_planos_y_fuente_de_tensi%C3%B3n"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace