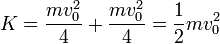Dos partículas unidas por una barra
De Laplace
(→Movimiento de cada partícula) |
|||
| (13 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que | + | Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial <math>v_0</math> perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra? |
==Estado inicial== | ==Estado inicial== | ||
El movimiento de ambas partículas va a ser en todo momento sobre el plano. Si tomamos un sistema de ejes cartesianos tal que el origen de coordenadas se encuentra en el centro de la posición inicial de la barra, y el eje X alineado con ella inicialmente, las posiciones de partida de ambas partículas son | El movimiento de ambas partículas va a ser en todo momento sobre el plano. Si tomamos un sistema de ejes cartesianos tal que el origen de coordenadas se encuentra en el centro de la posición inicial de la barra, y el eje X alineado con ella inicialmente, las posiciones de partida de ambas partículas son | ||
| - | <center><math>\ | + | <center><math>\vec{r}_{10}=-\frac{b}{2}\vec{\imath}</math>{{qquad}}{{qquad}}<math>\vec{r}_{20}=\frac{b}{2}\vec{\imath}</math></center> |
mientras que las velocidades iniciales valen | mientras que las velocidades iniciales valen | ||
| - | <center><math>\ | + | <center><math>\vec{v}_{10}=\vec{0}</math>{{qquad}}{{qquad}}<math>\vec{v}_{20}=v_0\vec{\jmath}</math></center> |
A partir de aquí obtenemos la posición y la velocidad inicial del centro de masas | A partir de aquí obtenemos la posición y la velocidad inicial del centro de masas | ||
| - | <center><math>\ | + | <center><math>\vec{r}_{C0} = \frac{m\vec{r}_{10}+m\vec{r}_{20}}{2m} = \vec{0}</math>{{qquad}}{{qquad}}<math>\vec{v}_{C0} = \frac{m\vec{v}_{10}+m\vec{v}_{20}}{2m} = \frac{v_0}{2}\vec{\jmath}</math></center> |
==Movimiento del centro de masas== | ==Movimiento del centro de masas== | ||
| Línea 20: | Línea 20: | ||
De la conservación de la cantidad de movimiento del sistema se deduce que el centro de masas se mueve con movimiento rectilíneo y uniforme | De la conservación de la cantidad de movimiento del sistema se deduce que el centro de masas se mueve con movimiento rectilíneo y uniforme | ||
| - | <center><math>\ | + | <center><math>\vec{r}_C = \vec{r}_{C0}+\vec{v}_{C0}t = \frac{v_0t}{2}\vec{\jmath}</math></center> |
Geométricamente esto significa que el centro de la barra se mueve uniformemente y la barra gira en torno a su centro, de una manera que aun hemos de determinar. | Geométricamente esto significa que el centro de la barra se mueve uniformemente y la barra gira en torno a su centro, de una manera que aun hemos de determinar. | ||
| Línea 29: | Línea 29: | ||
El momento angular inicial vale | El momento angular inicial vale | ||
| - | <center><math>\ | + | <center><math>\vec{L}_0= m_1\vec{r}_{10}\times\vec{v}_{10}+m_2\vec{r}_{20}\times\vec{v}_{20} = m\left(\frac{b}{2}\vec{\imath}\right)\times\left(v_0\vec{\jmath}\right) = \frac{mbv_0}{2}\vec{k}</math></center> |
| + | |||
| + | Esta cantidad es una constante de movimiento, por lo que, en todo momento | ||
| + | |||
| + | <center><math>\vec{r}_{1}\times\vec{v}_{1}+\vec{r}_{2}\times\vec{v}_{2} =\frac{\vec{L}}{m}= \frac{bv_0}{2}\vec{k}</math></center> | ||
| + | |||
| + | Para simplificar el problema empleamos la posición relativa al centro de masas. Definimos | ||
| + | |||
| + | <center><math>\vec{r}\equiv\vec{r}'_2 = \vec{r}_2-\vec{r}_C</math></center> | ||
| + | |||
| + | Se cumple, por ser posiciones relativas de dos partículas de la misma masa | ||
| + | |||
| + | <center><math>\vec{r}'_1 = -\vec{r}\,</math>{{qquad}}{{qquad}}<math>\vec{v} = \vec{v}'_2 = \vec{v}_2-\vec{v}_C</math>{{qquad}}{{qquad}}<math>\vec{v}'_1=-\vec{v}\,</math></center> | ||
| + | |||
| + | Esto reduce la ley de conservación del momento angular a | ||
| + | |||
| + | <center><math>\vec{r}\times\vec{v} = \frac{bv_0}{4}\vec{k}</math></center> | ||
| + | |||
| + | Si empleamos coordenadas polares vemos que esta ecuación equivale a la conservación de la velocidad areolar | ||
| + | |||
| + | <center><math>\vec{r}=\rho\vec{u}_\rho\,</math>{{qquad}}{{qquad}}<math>\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\,\dot{\varphi}\,\vec{u}_\varphi</math>{{qquad}}{{qquad}}<math>\vec{r}\times\vec{v} = \rho^2\dot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | lo que nos da la ecuación | ||
| + | |||
| + | <center><math>\rho^2\dot{\varphi} = \frac{bv_0}{4}</math></center> | ||
| + | |||
| + | La cantidad <math>\rho</math> es el módulo del vector de posición relativa <math>\vec{r}</math>. Esta cantidad es constante e igual a la mitad de la longitud de la barra. Por ello, nos queda | ||
| + | |||
| + | <center><math>\dot{\varphi}=\frac{v_0}{b}=\omega =\mathrm{cte.}</math></center> | ||
| + | |||
| + | lo que nos dice que el ángulo <math>\varphi</math> crece uniformemente, esto es, que el vector de posición relativa rota uniformemente | ||
| + | |||
| + | <center><math>\varphi = \omega t+\varphi_0=\frac{v_0t}{b}</math></center> | ||
| + | |||
| + | El valor inicial <math>\varphi_0=0</math> es nulo por estar la barra inicialmente alineada con el eje X. | ||
| + | |||
| + | A partir de aquí obtenemos la posición de cada una de las masas | ||
| + | |||
| + | <center><math>\vec{r}= \frac{b}{2}\cos\left(\frac{v_0t}{b}\right)\vec{\imath}+\frac{b}{2}\,\mathrm{sen}\,\left(\frac{v_0t}{b}\right)\vec{\jmath}</math></center> | ||
| + | |||
| + | <center><math>\vec{r}_1 = \vec{r}_C-\vec{r}= -\frac{b}{2}\cos\left(\frac{v_0t}{b}\right)\vec{\imath}+\left(\frac{v_0t}{2}-\frac{b}{2}\,\mathrm{sen}\,\left(\frac{v_0t}{b}\right)\right)\vec{\jmath}</math></center> | ||
| + | |||
| + | <center><math>\vec{r}_2 = \vec{r}_C+\vec{r}= \frac{b}{2}\cos\left(\frac{v_0t}{b}\right)\vec{\imath}+\left(\frac{v_0t}{2}+\frac{b}{2}\,\mathrm{sen}\,\left(\frac{v_0t}{b}\right)\right)\vec{\jmath}</math></center> | ||
| + | |||
| + | Cada una de las partículas describe una cicloide, y el movimiento de la barra es el mismo que tendría un diámetro de un disco que rodara sin deslizar. | ||
| + | |||
| + | <center>[[Imagen:barrarotante.gif]]</center> | ||
| + | |||
| + | Derivando en las expresiones anteriores se obtiene la velocidad relativa y la de cada partícula | ||
| + | |||
| + | <center><math>\vec{v}= -\frac{v_0}{2}\,\mathrm{sen}\left(\frac{v_0t}{b}\right)\vec{\imath}+\frac{v_0}{2}\cos\left(\frac{v_0t}{b}\right)\vec{\jmath}</math></center> | ||
| + | |||
| + | <center><math>\vec{v}_1 = \vec{v}_C-\vec{v}= \frac{v_0}{2}\,\mathrm{sen}\left(\frac{v_0t}{b}\right)\vec{\imath}+\frac{v_0}{2}\left(1-\cos\left(\frac{v_0t}{b}\right)\right)\vec{\jmath}</math></center> | ||
| + | |||
| + | <center><math>\vec{v}_2 = \vec{v}_C+\vec{v}= -\frac{v_0}{2}\,\mathrm{sen}\left(\frac{v_0t}{b}\right)\vec{\imath}+\frac{v_0}{2}\left(1+\cos\left(\frac{v_0t}{b}\right)\right)\vec{\jmath}</math></center> | ||
==Energía cinética del sistema== | ==Energía cinética del sistema== | ||
| + | La energía cinética asociada a la traslación del CM es | ||
| + | |||
| + | <center><math>K_C = \frac{1}{2}(2m)v_C^2 = \frac{mv_0^2}{4}</math></center> | ||
| + | |||
| + | mientras que la debida a la rotación alrededor de él vale | ||
| + | |||
| + | <center><math>K' = 2\left(\frac{1}{2}mv^2\right) = m\left(\left(\frac{v_0}{2}\,\mathrm{sen}(\omega t)\right)^2+\left(\frac{v_0}{2}\cos(\omega t)\right)^2\right) = \frac{mv_0^2}{4}</math></center> | ||
| + | |||
| + | En este sistema (un ''sólido rígido'') sí se cumple la conservación de la energía cinética que en este caso se divide en dos partes iguales debidas a la traslación y a la rotación | ||
| + | |||
| + | <center><math>K = \frac{mv_0^2}{4}+\frac{mv_0^2}{4} = \frac{1}{2}mv_0^2</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de dinámica de un sistema de partículas]] | ||
última version al 12:32 14 dic 2015
Contenido |
1 Enunciado
Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial v0 perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?
2 Estado inicial
El movimiento de ambas partículas va a ser en todo momento sobre el plano. Si tomamos un sistema de ejes cartesianos tal que el origen de coordenadas se encuentra en el centro de la posición inicial de la barra, y el eje X alineado con ella inicialmente, las posiciones de partida de ambas partículas son
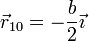
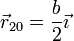
mientras que las velocidades iniciales valen
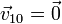
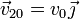
A partir de aquí obtenemos la posición y la velocidad inicial del centro de masas
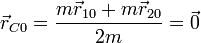
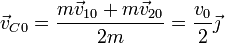
3 Movimiento del centro de masas
En este sistema todas las fuerzas son internas, y se ejercen mediante la tensión de la barra, que funciona como un resorte de longitud natural a y constante de recuperación infinita. Por ello se conservan tanto la cantidad de movimiento como el momento cinético del sistema.
De la conservación de la cantidad de movimiento del sistema se deduce que el centro de masas se mueve con movimiento rectilíneo y uniforme
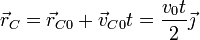
Geométricamente esto significa que el centro de la barra se mueve uniformemente y la barra gira en torno a su centro, de una manera que aun hemos de determinar.
4 Movimiento de cada partícula
Para determinar cómo se mueven las partículas situadas en los extremos de la barra aplicamos la conservación del momento angular del sistema.
El momento angular inicial vale
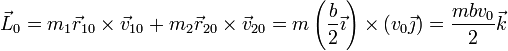
Esta cantidad es una constante de movimiento, por lo que, en todo momento
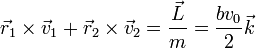
Para simplificar el problema empleamos la posición relativa al centro de masas. Definimos
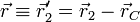
Se cumple, por ser posiciones relativas de dos partículas de la misma masa
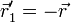
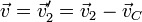
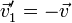
Esto reduce la ley de conservación del momento angular a
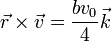
Si empleamos coordenadas polares vemos que esta ecuación equivale a la conservación de la velocidad areolar
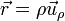
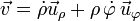
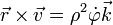
lo que nos da la ecuación
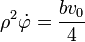
La cantidad ρ es el módulo del vector de posición relativa  . Esta cantidad es constante e igual a la mitad de la longitud de la barra. Por ello, nos queda
. Esta cantidad es constante e igual a la mitad de la longitud de la barra. Por ello, nos queda
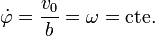
lo que nos dice que el ángulo  crece uniformemente, esto es, que el vector de posición relativa rota uniformemente
crece uniformemente, esto es, que el vector de posición relativa rota uniformemente
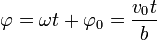
El valor inicial 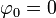 es nulo por estar la barra inicialmente alineada con el eje X.
es nulo por estar la barra inicialmente alineada con el eje X.
A partir de aquí obtenemos la posición de cada una de las masas
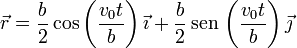
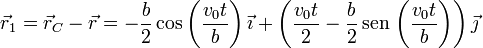
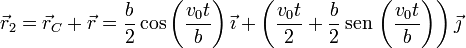
Cada una de las partículas describe una cicloide, y el movimiento de la barra es el mismo que tendría un diámetro de un disco que rodara sin deslizar.

Derivando en las expresiones anteriores se obtiene la velocidad relativa y la de cada partícula
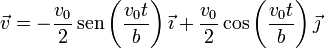
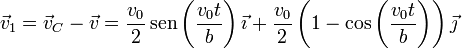
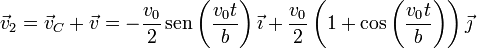
5 Energía cinética del sistema
La energía cinética asociada a la traslación del CM es
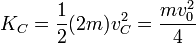
mientras que la debida a la rotación alrededor de él vale
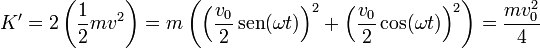
En este sistema (un sólido rígido) sí se cumple la conservación de la energía cinética que en este caso se divide en dos partes iguales debidas a la traslación y a la rotación