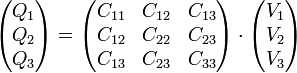Sistema de cuatro conductores prismáticos

De Laplace

Revisión de 09:43 10 ene 2009 (ver código fuente) Antonio (Discusión | contribuciones) (→Solución) ← Edición más antigua		Revisión de 09:55 10 ene 2009 (ver código fuente) Antonio (Discusión | contribuciones) (→Carga en cada conductor) Edición más nueva →
Línea 10:		Línea 10:
	==Solución==		==Solución==
	===Carga en cada conductor===		===Carga en cada conductor===
		+	Lo que se pide en este apartado es hallar la carga en cada conductor conocidas las tensiones de cada uno. Para calcularlas necesitamos los coeficientes de capacidad, que relacionan ambas magnitudes en forma matricial
		+
		+	<center><math>\begin{pmatrix}Q_1 \\ Q_2 \\ Q_3\end{pmatrix} = \begin{pmatrix}C_{11} & C_{12} & C_{13}\\ C_{12} & C_{22} & C_{23} \\ C_{13} & C_{23} & C_{33}\end{pmatrix}\cdot \begin{pmatrix}V_1 \\ V_2 \\ V_3\end{pmatrix}</math></center>
		+
	===Energía almacenada===		===Energía almacenada===
	===Cargas y potenciales===		===Cargas y potenciales===
	[[Categoría:Problemas de campo eléctrico en presencia de conductores]]		[[Categoría:Problemas de campo eléctrico en presencia de conductores]]

---

Revisión de 09:55 10 ene 2009

Contenido 1 Enunciado 2 Solución 2.1 Carga en cada conductor 2.2 Energía almacenada 2.3 Cargas y potenciales

1 Enunciado

Se tiene un sistema de cuatro conductores tal como se indica en la figura. Uno de ellos (conductor “4”) es un prisma cuadrado hueco de lado 43 mm y longitud 50 mm. Este conductor se encuentra siempre a tierra.

En su interior se encuentran tres conductores. El conductor “1” es un paralelepípedo de lados 41 mm, 20 mm y 50 mm. Los conductores “2” y “3” son sendos prismas cuadrados de lado 20 mm y altura 50 mm. la distancia entre superficies conductoras vecinas es de 1 mm.

1. Teniendo en cuenta la pequeñez relativa de las diferentes distancias calcule, aproximadamente, las cargas que almacenan los conductores 1, 2 y 3, cuando sus tensiones son 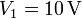, 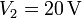y .
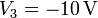2. Para la configuración anterior, calcule la energía electrostática almacenada en el sistema.
3. Si el conductor 1 se encuentra a tensión 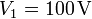, el 2 aislado y descargado y el 3 a tierra, ¿cuáles son las cargas y los potenciales de los tres conductores? ¿Y la energía electrostática almacenada en el sistema?

2 Solución

2.1 Carga en cada conductor

Lo que se pide en este apartado es hallar la carga en cada conductor conocidas las tensiones de cada uno. Para calcularlas necesitamos los coeficientes de capacidad, que relacionan ambas magnitudes en forma matricial

2.2 Energía almacenada

2.3 Cargas y potenciales