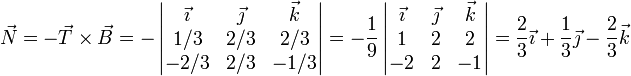Entrar Página Discusión Historial Go to the site toolbox

Construcción de una base

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Primer vector== Obtenemos el primer vector normalizando el vector <math>\vec{v}</math>, esto es, hallando el unitario en su dirección y sentido, lo que se consigue dividiendo…')
 
(3 ediciones intermedias no se muestran.)
Línea 1: Línea 1:
 +
==Enunciado==
 +
Dados los vectores
 +
 +
<center><math>\vec{v}=\vec{\imath}+2\vec{\jmath}+2\vec{k}\qquad\qquad\vec{a}=6\vec{\imath}+9\vec{\jmath}+6\vec{k}</math></center>
 +
 +
Construya una base ortonormal dextrógira <math>\{\vec{T},\vec{N},\vec{B}\}</math>, tal que
 +
 +
# El primer vector, <math>\vec{T}</math>, vaya en la dirección y sentido de <math>\vec{v}</math>
 +
# El segundo, <math>\vec{N}</math>, esté contenido en el plano definido por <math>\vec{v}</math> y <math>\vec{a}</math> y apunte hacia el mismo semiplano (respecto de <math>\vec{v}</math>) que el vector <math>\vec{a}</math>.
 +
# El tercero, <math>\vec{B}</math>, sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
 +
==Primer vector==
==Primer vector==
Obtenemos el primer vector normalizando el vector <math>\vec{v}</math>, esto es, hallando el unitario en su dirección y sentido, lo que se consigue dividiendo este vector por su módulo
Obtenemos el primer vector normalizando el vector <math>\vec{v}</math>, esto es, hallando el unitario en su dirección y sentido, lo que se consigue dividiendo este vector por su módulo
-
<center><math>\vec{u}_1=\frac{\vec{v}}{v}</math></center>
+
<center><math>\vec{T}=\frac{\vec{v}}{|\vec{v}|}</math></center>
Hallamos el módulo de <math>\vec{v}</math>
Hallamos el módulo de <math>\vec{v}</math>
-
<center><math>v = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{1^2+2^2+2^2}=3</math></center>
+
<center><math> \left|\vec{v}\right| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{1^2+2^2+2^2}=3</math></center>
por lo que
por lo que
-
<center><math>\vec{u}_1 = \frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}+\frac{2}{3}\vec{k}</math></center>
+
<center><math>\vec{T} = \frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}+\frac{2}{3}\vec{k}</math></center>
==Segundo vector==
==Segundo vector==
El segundo vector debe estar en el plano definido por <math>\vec{v}</math> y <math>\vec{a}</math>, por lo que debe ser una combinación lineal de ambos
El segundo vector debe estar en el plano definido por <math>\vec{v}</math> y <math>\vec{a}</math>, por lo que debe ser una combinación lineal de ambos
-
<center><math>\vec{u}_2 = \lambda\vec{v}+\mu\vec{a}</math></center>
+
<center><math>\vec{N} = \lambda\vec{v}+\mu\vec{a}</math></center>
-
además debe ser ortogonal a <math>\vec{u}_1</math> (y por tanto, a <math>\vec{v}</math>)
+
además debe ser ortogonal a <math>\vec{T}</math> (y por tanto, a <math>\vec{v}</math>)
-
<center><math>\vec{u}_2\cdot\vec{u}_1 = 0 = \vec{u}_2\cdot\vec{v}</math></center>
+
<center><math>\vec{N}\cdot\vec{T} = 0 = \vec{N}\cdot\vec{v}</math></center>
y debe ser unitario
y debe ser unitario
-
<center><math>\vec{u}_2\cdot\vec{u}_2=1</math></center>
+
<center><math>\vec{N}\cdot\vec{N}=1</math></center>
El procedimiento sistemático consiste en hallar la componente de <math>\vec{a}</math> perpendicular a <math>\vec{v}</math> y posteriormente normalizar el resultado.
El procedimiento sistemático consiste en hallar la componente de <math>\vec{a}</math> perpendicular a <math>\vec{v}</math> y posteriormente normalizar el resultado.
-
La proyección normal la calculamos con ayuda del [[Vectores_libres_(G.I.T.I.)#Doble_producto_vectorial|doble producto vectorial]]
+
La proyección normal la calculamos con ayuda del [[Vectores_en_física_(GIE)#Doble_producto_vectorial|doble producto vectorial]]
-
<center><math>\vec{a}_n = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{v^2}</math></center>
+
<center><math>\vec{a}_n = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{|\vec{v}|^2}</math></center>
Calculamos el primer producto vectorial
Calculamos el primer producto vectorial
Línea 37: Línea 48:
Hallamos el segundo
Hallamos el segundo
-
<center><math>(\vec{a}\times\vec{v})\times \vec{v}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -6 & 6 & -3 \\ 1 & 2 & 2  \end{matrix}\right|=18\vec{\imath}+9\vec{\jmath}-18\vec{k}</math></center>
+
<center><math>(\vec{v}\times\vec{a})\times \vec{v}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -6 & 6 & -3 \\ 1 & 2 & 2  \end{matrix}\right|=18\vec{\imath}+9\vec{\jmath}-18\vec{k}</math></center>
Dividiendo por el módulo de <math>\vec{v}</math> al cuadrado  obtenemos la componente normal
Dividiendo por el módulo de <math>\vec{v}</math> al cuadrado  obtenemos la componente normal
Línea 45: Línea 56:
Alternativamente, podemos hallar esta proyección ortogonal restando al vector completo la parte paralela
Alternativamente, podemos hallar esta proyección ortogonal restando al vector completo la parte paralela
-
<center><math>\vec{a}_n = \vec{a}-(\vec{a}\cdot\vec{u}_1)\vec{u}_1</math></center>
+
<center><math>\vec{a}_n = \vec{a}-(\vec{a}\cdot\vec{T})\vec{T}</math></center>
Normalizando esta cantidad obtenemos el segundo vector de la base
Normalizando esta cantidad obtenemos el segundo vector de la base
-
<center><math>\vec{u}_2 = \frac{\vec{a}_n}{a_n}=\frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}</math></center>
+
<center><math>\vec{N} = \frac{\vec{a}_n}{|\vec{a}_n|}=\frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}</math></center>
==Tercer vector==
==Tercer vector==
El tercer vector lo obtenemos como el producto vectorial de los dos primeros
El tercer vector lo obtenemos como el producto vectorial de los dos primeros
-
<center><math>\vec{u}_3=\vec{u}_1\times\vec{u}_2=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1/3 & 2/3 & 2/3 \\ 2/3 & 1/3 & -2/3\end{matrix}\right|=\frac{1}{9}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ 2 & 1 & -2\end{matrix}\right| = -\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}</math></center>
+
<center><math>\vec{B}=\vec{T}\times\vec{N}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1/3 & 2/3 & 2/3 \\ 2/3 & 1/3 & -2/3\end{matrix}\right|=\frac{1}{9}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ 2 & 1 & -2\end{matrix}\right| = -\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}</math></center>
Por tanto, la base ortonormal dextrógira está formada por los vectores
Por tanto, la base ortonormal dextrógira está formada por los vectores
Línea 60: Línea 71:
<center><math>
<center><math>
\begin{array}{lcr}
\begin{array}{lcr}
-
\vec{u}_1 & = & \displaystyle\frac{1}{3}\vec{\imath}+\displaystyle\frac{2}{3}\vec{\jmath}+\displaystyle\frac{2}{3}\vec{k}\\&& \\
+
\vec{T} & = & \displaystyle\frac{1}{3}\vec{\imath}+\displaystyle\frac{2}{3}\vec{\jmath}+\displaystyle\frac{2}{3}\vec{k}\\&& \\
-
\vec{u}_2 & = & \displaystyle\frac{2}{3}\vec{\imath}+\displaystyle\frac{1}{3}\vec{\jmath}-\displaystyle\frac{2}{3}\vec{k}\\&& \\
+
\vec{N} & = & \displaystyle\frac{2}{3}\vec{\imath}+\displaystyle\frac{1}{3}\vec{\jmath}-\displaystyle\frac{2}{3}\vec{k}\\&& \\
-
\vec{u}_3 & = & -\displaystyle\frac{2}{3}\vec{\imath}+\displaystyle\frac{2}{3}\vec{\jmath}-\displaystyle\frac{1}{3}\vec{k}
+
\vec{B} & = & -\displaystyle\frac{2}{3}\vec{\imath}+\displaystyle\frac{2}{3}\vec{\jmath}-\displaystyle\frac{1}{3}\vec{k}
\end{array}</math></center>
\end{array}</math></center>
Línea 70: Línea 81:
El tercer vector de la base es ortogonal a los dos primeros. También es ortogonal a cualquier combinación lineal de los dos primeros, en particular a los dos vectores del enunciado <math>\vec{v}</math> y <math>\vec{a}</math>. Por ello, podemos calcular el tercer vector como
El tercer vector de la base es ortogonal a los dos primeros. También es ortogonal a cualquier combinación lineal de los dos primeros, en particular a los dos vectores del enunciado <math>\vec{v}</math> y <math>\vec{a}</math>. Por ello, podemos calcular el tercer vector como
-
<center><math>\vec{u}_3 = \frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}</math></center>
+
<center><math>\vec{B} = \frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}</math></center>
El producto vectorial vale
El producto vectorial vale
Línea 82: Línea 93:
resultando el unitario
resultando el unitario
-
<center><math>\vec{u}_3 = -\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}</math></center>
+
<center><math>\vec{B} = -\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}</math></center>
El segundo vector lo obtenemos del producto vectorial del primero y el tercero, teniendo en cuenta el cambio de signo debido a la inversión del orden
El segundo vector lo obtenemos del producto vectorial del primero y el tercero, teniendo en cuenta el cambio de signo debido a la inversión del orden
-
<center><math>\vec{u}_2 = -\vec{u}_1\times\vec{u}_3 = -\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1/3 & 2/3 & 2/3 \\ -2/3 & 2/3 & -1/3\end{matrix}\right|=-\frac{1}{9}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ -2 & 2 & -1\end{matrix}\right| = \frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}</math></center>
+
<center><math>\vec{N} = -\vec{T}\times\vec{B} = -\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1/3 & 2/3 & 2/3 \\ -2/3 & 2/3 & -1/3\end{matrix}\right|=-\frac{1}{9}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ -2 & 2 & -1\end{matrix}\right| = \frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}</math></center>
[[Categoría:Problemas de herramientas matemáticas (GIE)]]
[[Categoría:Problemas de herramientas matemáticas (GIE)]]

última version al 11:48 1 oct 2015

Contenido

1 Enunciado

Dados los vectores

\vec{v}=\vec{\imath}+2\vec{\jmath}+2\vec{k}\qquad\qquad\vec{a}=6\vec{\imath}+9\vec{\jmath}+6\vec{k}

Construya una base ortonormal dextrógira 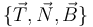\{\vec{T},\vec{N},\vec{B}\}, tal que

  1. El primer vector, \vec{T}, vaya en la dirección y sentido de \vec{v}
  2. El segundo, \vec{N}, esté contenido en el plano definido por \vec{v} y \vec{a} y apunte hacia el mismo semiplano (respecto de \vec{v}) que el vector \vec{a}.
  3. El tercero, \vec{B}, sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.

2 Primer vector

Obtenemos el primer vector normalizando el vector \vec{v}, esto es, hallando el unitario en su dirección y sentido, lo que se consigue dividiendo este vector por su módulo

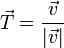
\vec{T}=\frac{\vec{v}}{|\vec{v}|}

Hallamos el módulo de \vec{v}

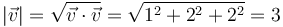
\left|\vec{v}\right| = \sqrt{\vec{v}\cdot\vec{v}}=\sqrt{1^2+2^2+2^2}=3

por lo que

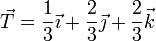
\vec{T} = \frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}+\frac{2}{3}\vec{k}

3 Segundo vector

El segundo vector debe estar en el plano definido por \vec{v} y \vec{a}, por lo que debe ser una combinación lineal de ambos

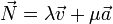
\vec{N} = \lambda\vec{v}+\mu\vec{a}

además debe ser ortogonal a \vec{T} (y por tanto, a \vec{v})

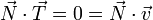
\vec{N}\cdot\vec{T} = 0 = \vec{N}\cdot\vec{v}

y debe ser unitario

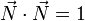
\vec{N}\cdot\vec{N}=1

El procedimiento sistemático consiste en hallar la componente de \vec{a} perpendicular a \vec{v} y posteriormente normalizar el resultado.

La proyección normal la calculamos con ayuda del doble producto vectorial

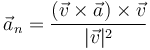
\vec{a}_n = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{|\vec{v}|^2}

Calculamos el primer producto vectorial

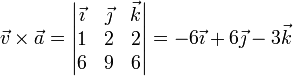
\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2\\ 6 & 9 & 6\end{matrix}\right|=-6\vec{\imath}+6\vec{\jmath}-3\vec{k}

Hallamos el segundo

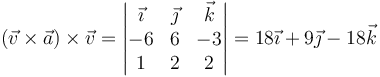
(\vec{v}\times\vec{a})\times \vec{v}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -6 & 6 & -3 \\ 1 & 2 & 2 \end{matrix}\right|=18\vec{\imath}+9\vec{\jmath}-18\vec{k}

Dividiendo por el módulo de \vec{v} al cuadrado obtenemos la componente normal

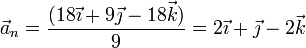
\vec{a}_n = \frac{(18\vec{\imath}+9\vec{\jmath}-18\vec{k})}{9}=2\vec{\imath}+\vec{\jmath}-2\vec{k}

Alternativamente, podemos hallar esta proyección ortogonal restando al vector completo la parte paralela

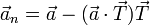
\vec{a}_n = \vec{a}-(\vec{a}\cdot\vec{T})\vec{T}

Normalizando esta cantidad obtenemos el segundo vector de la base

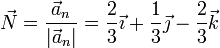
\vec{N} = \frac{\vec{a}_n}{|\vec{a}_n|}=\frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}

4 Tercer vector

El tercer vector lo obtenemos como el producto vectorial de los dos primeros

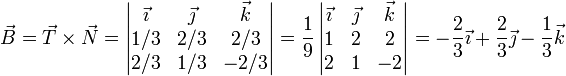
\vec{B}=\vec{T}\times\vec{N}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1/3 & 2/3 & 2/3 \\ 2/3 & 1/3 & -2/3\end{matrix}\right|=\frac{1}{9}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ 2 & 1 & -2\end{matrix}\right| = -\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}

Por tanto, la base ortonormal dextrógira está formada por los vectores

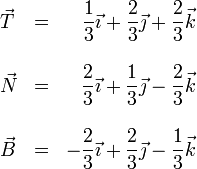
\begin{array}{lcr} \vec{T} & = & \displaystyle\frac{1}{3}\vec{\imath}+\displaystyle\frac{2}{3}\vec{\jmath}+\displaystyle\frac{2}{3}\vec{k}\\&& \\ \vec{N} & = & \displaystyle\frac{2}{3}\vec{\imath}+\displaystyle\frac{1}{3}\vec{\jmath}-\displaystyle\frac{2}{3}\vec{k}\\&& \\ \vec{B} & = & -\displaystyle\frac{2}{3}\vec{\imath}+\displaystyle\frac{2}{3}\vec{\jmath}-\displaystyle\frac{1}{3}\vec{k} \end{array}

5 Forma alternativa

Podemos acortar un poco el proceso invirtiendo el orden de cálculo.

El tercer vector de la base es ortogonal a los dos primeros. También es ortogonal a cualquier combinación lineal de los dos primeros, en particular a los dos vectores del enunciado \vec{v} y \vec{a}. Por ello, podemos calcular el tercer vector como

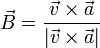
\vec{B} = \frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}

El producto vectorial vale

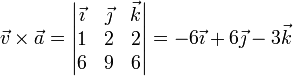
\vec{v}\times\vec{a} = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ 6 & 9 & 6\end{matrix}\right| = -6\vec{\imath}+6\vec{\jmath}-3\vec{k}

con módulo

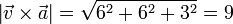
\left|\vec{v}\times\vec{a}\right| = \sqrt{6^2+6^2+3^2} = 9

resultando el unitario

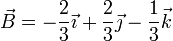
\vec{B} = -\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}

El segundo vector lo obtenemos del producto vectorial del primero y el tercero, teniendo en cuenta el cambio de signo debido a la inversión del orden

\vec{N} = -\vec{T}\times\vec{B} = -\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1/3 & 2/3 & 2/3 \\ -2/3 & 2/3 & -1/3\end{matrix}\right|=-\frac{1}{9}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1 & 2 & 2 \\ -2 & 2 & -1\end{matrix}\right| = \frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}
Obtenido de "http://tesla.us.es/wiki/index.php/Construcci%C3%B3n_de_una_base"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:48, 1 oct 2015. - Esta página ha sido visitada 2.843 veces. - Aviso legal - Acerca de Laplace