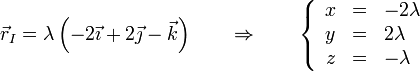Rodadura y pivotamiento de una pelota
De Laplace
(→Velocidades angulares) |
(→Posición del EIR) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 61: | Línea 61: | ||
==Posición del EIR== | ==Posición del EIR== | ||
| + | [[Archivo:bola-rueda-pivota-04.png|right]] | ||
| + | |||
El eje instantáneo de rotación está formado por todos los puntos que tienen velocidad nula. Consiste en una recta que pasa por alguno de los puntos en reposo instantáneo y tiene la dirección de la velocidad angular. | El eje instantáneo de rotación está formado por todos los puntos que tienen velocidad nula. Consiste en una recta que pasa por alguno de los puntos en reposo instantáneo y tiene la dirección de la velocidad angular. | ||
En este caso, ya conocemos un punto de velocidad nula: el origen O en que la bola toca el suelo. Por tanto, los puntos del eje son de la forma | En este caso, ya conocemos un punto de velocidad nula: el origen O en que la bola toca el suelo. Por tanto, los puntos del eje son de la forma | ||
| - | <center><math>\vec{r}_I = \vec{0}+\mu\vec{\omega} = \frac{\ | + | <center><math>\vec{r}_I = \vec{0}+\mu\vec{\omega} = \frac{\mu v_0}{R}\left(-2\vec{\imath}+2\vec{\jmath}-\vec{k}\right)</math></center> |
Haciendo <math>\lambda = \mu v_0/R</math> nos queda una expresión un poco más simple | Haciendo <math>\lambda = \mu v_0/R</math> nos queda una expresión un poco más simple | ||
| Línea 72: | Línea 74: | ||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
| + | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
última version al 10:48 24 sep 2015
Contenido |
1 Enunciado
Una pelota de radio R rueda y pivota sin deslizar sobre el plano horizontal z = 0, de forma que las velocidades de los puntos  y
y  valen respectivamente
valen respectivamente 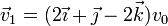 y
y  .
.
- Determine la velocidad angular de rodadura y la de pivotamiento.
- Halle la velocidad del centro de la bola.
- Determine la ecuación del eje instantáneo de rotación.
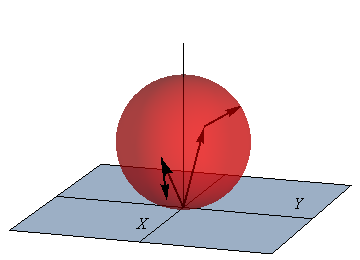
2 Velocidades angulares
Conocemos la velocidad de tres puntos del sólido: las dos que nos da explícitamente y la velocidad del punto de contacto de la bola con el suelo (el origen de coordenadas).
Puesto que nos dicen que rueda y pivota, pero no desliza, la velocidad de dicho punto es nula

Podemos hallar la velocidad resolviendo un sistema de ecuaciones lineales. Suponemos una velocidad angular desconocida
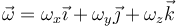
y aplicando la expresión del campo de velocidades respecto al punto O.
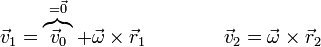
Aplicando esto al primer punto
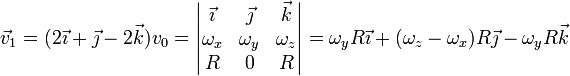
Igualando los dos vectores componente a componente
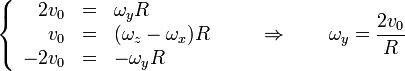
Para obtener las otras dos componentes precisamos, además de la ecuación que ya tenemos, la correspondiente al tercer punto
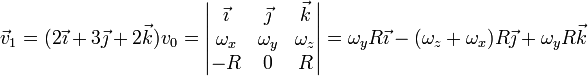
Llegamos así al sistema
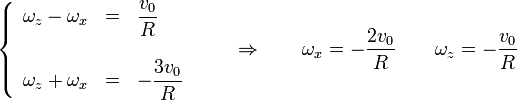
Reuniendo las tres componentes obtenemos el vector velocidad angular
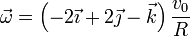
Esta velocidad angular es suma de la de pivotamiento y la de rodadura.
- Velocidad angular de pivotamiento
- es la componente perpendicular al plano de contacto

- Velocidad angular de rodadura
- es la parte paralela a la superficie de contacto.
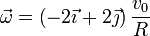
3 Velocidad del centro
Una vez que tenemos la velocidad de un punto de referencia y la velocidad angular del sólido, podemos hallar la velocidad instantánea de cualquier otro punto. Así para el centro
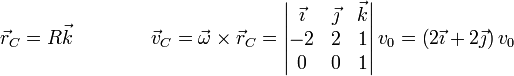
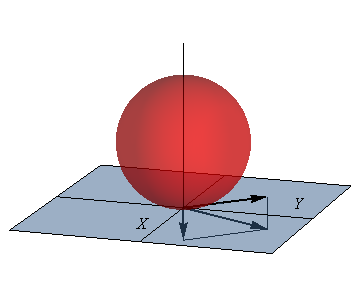
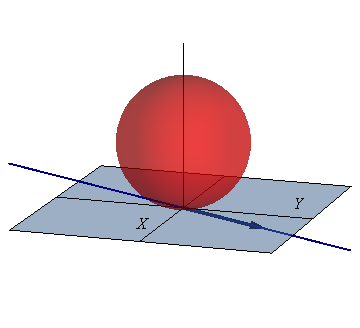
4 Posición del EIR
El eje instantáneo de rotación está formado por todos los puntos que tienen velocidad nula. Consiste en una recta que pasa por alguno de los puntos en reposo instantáneo y tiene la dirección de la velocidad angular.
En este caso, ya conocemos un punto de velocidad nula: el origen O en que la bola toca el suelo. Por tanto, los puntos del eje son de la forma
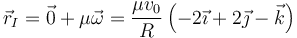
Haciendo λ = μv0 / R nos queda una expresión un poco más simple