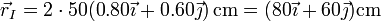Movimiento de un sistema biela-manivela
De Laplace
(→Aplicación numérica) |
|||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 15: | Línea 15: | ||
<center><math>\vec{r}_A = L\cos(\theta)\vec{\imath}+L\,\mathrm{sen}(\theta)\vec{\jmath}</math></center> | <center><math>\vec{r}_A = L\cos(\theta)\vec{\imath}+L\,\mathrm{sen}(\theta)\vec{\jmath}</math></center> | ||
| + | donde hemos elegido un sistema de referencia centrado en O, cuyo eje X es el eje fijo “1” y cuyo eje Y es el normal a él. | ||
| + | |||
| + | Derivando la posición de A respecto al tiempo obtenemos su velocidad | ||
| + | |||
| + | <center><math>\vec{v}_A = \frac{\mathrm{d}\vec{r}_A}{\mathrm{d}t}= \frac{\mathrm{d}\vec{r}_A}{\mathrm{d}\theta}\dot{\theta} = -L\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath}+L\dot{\theta}\cos(\theta)\vec{\jmath}</math></center> | ||
| + | |||
| + | ===Velocidad de B=== | ||
| + | Para calcular la velocidad de B, determinamos en primer lugar su posición. El triángulo OAB es isósceles, por lo que el ángulo que forma la biela con el eje es también <math>\theta</math>. Por tanto | ||
| + | |||
| + | <center><math>\vec{r}_B = 2L\cos(\theta)\vec{\imath}</math></center> | ||
| + | |||
| + | Derivando aquí respecto al tiempo | ||
| + | |||
| + | <center><math>\vec{v}_B = -2L\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath}</math></center> | ||
| + | |||
| + | Vemos que mientras que el extremo A describe un movimiento circular uniforme, el B realiza un movimiento armónico simple. | ||
| + | |||
| + | <center>[[Archivo:biela-manivela-02.gif]]</center> | ||
==Velocidad angular== | ==Velocidad angular== | ||
| + | Una vez que tenemos la velocidad de dos partículas en un movimiento plano, podemos hallar la velocidad angular de múltiples formas. Una de ellas es empleando el teorema de Chasles | ||
| + | |||
| + | <center><math>\vec{v}_B-\vec{v}_A = \vec{\omega}\times(\vec{r}_B-\vec{r}_A)</math></center> | ||
| + | |||
| + | Sabemos que la velocidad angular es perpendicular al plano del movimiento, <math>\vec{\omega}=\omega\vec{k}</math>. Sustituyendo todos los valores conocidos | ||
| + | |||
| + | <center><math>(-2L\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath})-(-L\dot{\theta}\,\mathrm{sen}(\theta)\vec{\imath}+L\dot{\theta}\cos(\theta)\vec{\jmath}) = \omega\vec{k}\times(2L\cos(\theta)\vec{\imath}-(L\cos(\theta)\vec{\imath}+L\,\mathrm{sen}(\theta)\vec{\jmath}))</math></center> | ||
| + | |||
| + | Operamos en esta expresión y obtenemos | ||
| + | |||
| + | <center><math>-L\dot{\theta}\left(\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}\right) = \omega L\left(\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}\right)</math></center> | ||
| + | |||
| + | Igualando componente a componente llegamos, por partida doble, a que | ||
| + | |||
| + | <center><math>\omega=-\dot{\theta}\qquad\qquad\vec{\omega}=-\dot{\theta}\vec{k}</math></center> | ||
| + | |||
| + | Podemos entender este resultado simplemente observando que mientras la manivela gira hacia la izquierda, la biela gira hacia la derecha el mismo ángulo (aunque respecto a un centro diferente que ahora calcularemos). | ||
==Posición del CIR== | ==Posición del CIR== | ||
| + | La posición del centro instantáneo de rotación puede obtenerse tanto gráficamente como analíticamente. | ||
| + | |||
| + | ===Determinación gráfica=== | ||
| + | [[Archivo:Biela-manivela-cir.png|right]]Puesto que la velocidad del centro instantáneo de rotación es nula, se cumple, para todo punto del sólido | ||
| + | |||
| + | <center><math>\vec{v}_P = \vec{\omega}\times(\vec{r}_P-\vec{r}_I)</math></center> | ||
| + | |||
| + | Esto implica que el vector de posición relativa de I respecto de P es perpendicular a la velocidad de P. Por tanto, trazando las perpendiculares a las velocidades de dos punto y hallando su intersección obtenemos la posición del CIR. | ||
| + | |||
| + | En nuestro caso, sabemos que la velocidad de B es puramente a lo largo del eje, por lo que el CIR se encuentra sobre la recta perpendicular al eje que pasa por B. | ||
| + | |||
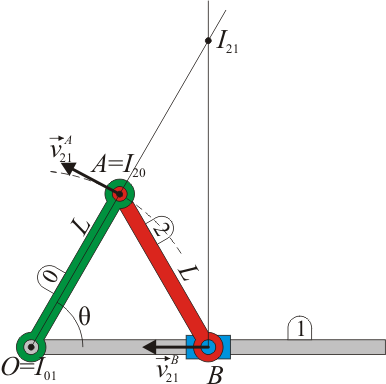
| + | El movimiento de A es circular, siendo su velocidad tangente a la circunferencia. El CIR se encuentra entonces en la recta radial que pasa por A. Esta recta es la prolongación de la manivela. La intersección de esta recta con la anterior nos da la posición del CIR <math>I_{21}</math>. Aparte de éste, existen otros dos CIR's: el <math>I_{20}</math> para el movimiento de la biela respecto a la manivela, y el <math>I_{01}</math> para el movimiento de la manivela respecto al eje. Estos dos centros coinciden con A y O, respectivamente. | ||
| + | |||
| + | Una vez que lo hemos determinado gráficamente, podemos expresar su posición de forma analítica. Por estar en la prolongación de la manivela, su posición es de la forma | ||
| + | |||
| + | <center><math>\vec{r}_I = \lambda(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath})</math></center> | ||
| + | |||
| + | y por estar en la vertical de B debe ser <math>x = 2L\cos(\theta)</math>. Esto nos da <math>\lambda = 2L</math> y la posición del CIR <math>I_{21}</math> | ||
| + | |||
| + | <center><math>\vec{r}_I = 2L(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath})</math></center> | ||
| + | |||
| + | ===Determinación analítica=== | ||
| + | Podemos determinar la posición del CIR de forma analítica recurriendo de nuevo a la ecuación | ||
| + | |||
| + | <center><math>\vec{v}_B = \vec{\omega}\times(\vec{r}_B-\vec{r}_I)</math></center> | ||
| + | |||
| + | Si en esta ecuación multiplicamos vectorialmente por <math>\vec{\omega}</math> nos queda | ||
| + | |||
| + | <center><math>\vec{\omega}\times\vec{v}_B = \vec{\omega}\times(\vec{\omega}\times(\vec{r}_B-\vec{r}_I)) = (\overbrace{(\vec{r}_B-\vec{r}_I)\cdot\vec{\omega}}^{=0})\vec{\omega}-|\vec{\omega}|^2(\vec{r}_B-\vec{r}_I)</math></center> | ||
| + | |||
| + | El término del último miembrose anula porque en un movimiento plano la velocidad angular es ortogonal a los vectores de posición y velocidad. Esto nos permite despejar y escribir | ||
| + | |||
| + | <center><math>\vec{r}_I = \vec{r}_B + \frac{\vec{\omega}\times\vec{v}_B}{|\vec{\omega}|^2}</math></center> | ||
| + | |||
| + | Sustituyendo las expresiones respectivas | ||
| + | |||
| + | <center><math>\vec{r}_I = 2L\cos(\theta)\vec{\imath}+\frac{-\dot{\theta}\vec{k}\times(-2L\dot{\theta}\mathrm{sen}(\theta)\vec{\imath})}{\dot{\theta}^2} = 2L(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath})</math></center> | ||
| + | |||
==Aplicación numérica== | ==Aplicación numérica== | ||
| + | Como caso particular tenemos un ángulo <math>\theta</math> tal que | ||
| + | |||
| + | <center><math>\mathrm{tg}(\theta) = 0.75\qquad\Rightarrow\qquad\mathrm{sen}(\theta) = 0.60\qquad\cos(\theta) = 0.80</math></center> | ||
| + | |||
| + | Sustituyendo obtenemos para las posiciones de A y B | ||
| + | |||
| + | <center><math>\vec{r}_A = 50(0.80\vec{\imath}+0.60\vec{\jmath})\,\mathrm{cm} = (40\vec{\imath}+30\vec{\jmath})\mathrm{cm}\qquad\qquad \vec{r}_B = 2\cdot 50(0.80\vec{\imath})\,\mathrm{cm} = (80\vec{\imath})\mathrm{cm}</math></center> | ||
| + | |||
| + | y para las velocidades, teniendo en cuenta que <math>\dot{\theta}=-2.00\,\mathrm{rad}/\mathrm{s}</math>, | ||
| + | |||
| + | <center><math>\vec{v}_A = 50\cdot(-2.00)(-0.60\vec{\imath}+0.80\vec{\jmath})\frac{\mathrm{cm}}{\mathrm{s}} = (60\vec{\imath}-80\vec{\jmath})\frac{\mathrm{cm}}{\mathrm{s}}\qquad\qquad \vec{v}_B = 2\cdot 50(-2.00)(0.60\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}} = (120\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | La velocidad angular de la biela respecto al eje es simplemente | ||
| + | |||
| + | <center><math>\vec{\omega} = (2.00\vec{k})\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | y, por último, la posición del CIR en este instante | ||
| + | |||
| + | <center><math>\vec{r}_I =2\cdot 50(0.80\vec{\imath}+0.60\vec{\jmath})\,\mathrm{cm} = (80\vec{\imath}+60\vec{\jmath})\mathrm{cm}</math></center> | ||
| + | |||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
| + | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
última version al 09:47 24 sep 2015
Contenido |
1 Enunciado
Un sistema biela-manivela está formado por: una barra fija (el eje “1”); una barra (la manivela “0”) de longitud L, articulada en el punto O del eje y que forma un ángulo θ(t) con él; y una segunda barra (la biela “2”), también de longitud L, articulada en el punto A de la manivela y cuyo segundo extremo B está obligado a deslizar por el eje.
- Halle las velocidades de los puntos A y B de la biela.
- Determine la velocidad angular de la biela respecto al eje.
- Localice el centro instantáneo de rotación (CIR) de la biela respecto al eje.
- Suponga el caso
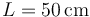 y que en un instante dado tg(θ) = 0.75 siendo
y que en un instante dado tg(θ) = 0.75 siendo 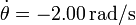 . Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.
. Calcule la velocidades respecto al eje de los puntos A y B de la biela, su velocidad angular y las coordenadas del CIR.
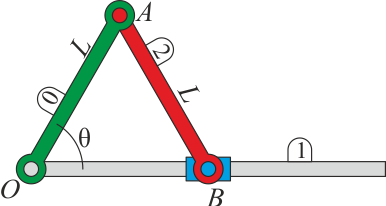
2 Velocidades de A y B
2.1 Velocidad de A
El punto A describe, respecto al eje fijo, un movimiento circular. Su posición en cada instante es
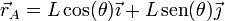
donde hemos elegido un sistema de referencia centrado en O, cuyo eje X es el eje fijo “1” y cuyo eje Y es el normal a él.
Derivando la posición de A respecto al tiempo obtenemos su velocidad
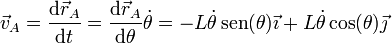
2.2 Velocidad de B
Para calcular la velocidad de B, determinamos en primer lugar su posición. El triángulo OAB es isósceles, por lo que el ángulo que forma la biela con el eje es también θ. Por tanto
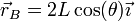
Derivando aquí respecto al tiempo
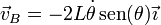
Vemos que mientras que el extremo A describe un movimiento circular uniforme, el B realiza un movimiento armónico simple.
3 Velocidad angular
Una vez que tenemos la velocidad de dos partículas en un movimiento plano, podemos hallar la velocidad angular de múltiples formas. Una de ellas es empleando el teorema de Chasles

Sabemos que la velocidad angular es perpendicular al plano del movimiento, 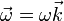 . Sustituyendo todos los valores conocidos
. Sustituyendo todos los valores conocidos
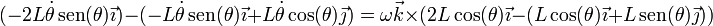
Operamos en esta expresión y obtenemos
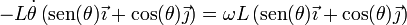
Igualando componente a componente llegamos, por partida doble, a que

Podemos entender este resultado simplemente observando que mientras la manivela gira hacia la izquierda, la biela gira hacia la derecha el mismo ángulo (aunque respecto a un centro diferente que ahora calcularemos).
4 Posición del CIR
La posición del centro instantáneo de rotación puede obtenerse tanto gráficamente como analíticamente.
4.1 Determinación gráfica
Puesto que la velocidad del centro instantáneo de rotación es nula, se cumple, para todo punto del sólido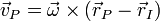
Esto implica que el vector de posición relativa de I respecto de P es perpendicular a la velocidad de P. Por tanto, trazando las perpendiculares a las velocidades de dos punto y hallando su intersección obtenemos la posición del CIR.
En nuestro caso, sabemos que la velocidad de B es puramente a lo largo del eje, por lo que el CIR se encuentra sobre la recta perpendicular al eje que pasa por B.
El movimiento de A es circular, siendo su velocidad tangente a la circunferencia. El CIR se encuentra entonces en la recta radial que pasa por A. Esta recta es la prolongación de la manivela. La intersección de esta recta con la anterior nos da la posición del CIR I21. Aparte de éste, existen otros dos CIR's: el I20 para el movimiento de la biela respecto a la manivela, y el I01 para el movimiento de la manivela respecto al eje. Estos dos centros coinciden con A y O, respectivamente.
Una vez que lo hemos determinado gráficamente, podemos expresar su posición de forma analítica. Por estar en la prolongación de la manivela, su posición es de la forma
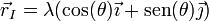
y por estar en la vertical de B debe ser x = 2Lcos(θ). Esto nos da λ = 2L y la posición del CIR I21
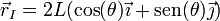
4.2 Determinación analítica
Podemos determinar la posición del CIR de forma analítica recurriendo de nuevo a la ecuación

Si en esta ecuación multiplicamos vectorialmente por  nos queda
nos queda
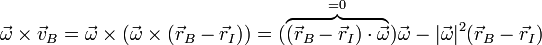
El término del último miembrose anula porque en un movimiento plano la velocidad angular es ortogonal a los vectores de posición y velocidad. Esto nos permite despejar y escribir

Sustituyendo las expresiones respectivas

5 Aplicación numérica
Como caso particular tenemos un ángulo θ tal que

Sustituyendo obtenemos para las posiciones de A y B
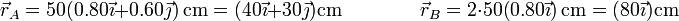
y para las velocidades, teniendo en cuenta que 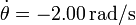 ,
,

La velocidad angular de la biela respecto al eje es simplemente
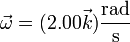
y, por último, la posición del CIR en este instante