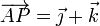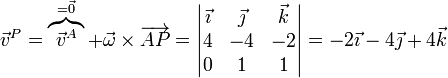Entrar Página Discusión Historial Go to the site toolbox

4.4. Sólido en rotación instantánea

De Laplace

(Diferencias entre revisiones)
(→Velocidad angular instantánea)
(→Velocidad del punto P)
 
(6 ediciones intermedias no se muestran.)
Línea 17: Línea 17:
y la velocidad de cualquier otro punto, en particular B, verifica
y la velocidad de cualquier otro punto, en particular B, verifica
-
<center><math>\vec{v}^B = \omega\times\overrightarrow{AB}</math></center>
+
<center><math>\vec{v}^B = \vec{\omega}\times\overrightarrow{AB}</math></center>
Esto implica que la velocidad de B es perpendicular a la velocidad angular, lo que nos proporciona una ecuación para la constante
Esto implica que la velocidad de B es perpendicular a la velocidad angular, lo que nos proporciona una ecuación para la constante
Línea 30: Línea 30:
Para hallar la velocidad angular, primero la escribimos como el producto de una componente escalar por el unitario en su dirección
Para hallar la velocidad angular, primero la escribimos como el producto de una componente escalar por el unitario en su dirección
-
<center><math>\vec{\omega} = \omega\frac{\vec{e}}{|vec{e}\,|}=\omega\left(\frac{2}{3}\vec{\imath}-\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}\right)</math></center>
+
<center><math>\vec{\omega} = \omega\frac{\vec{e}}{|\vec{e}\,|}=\omega\left(\frac{2}{3}\vec{\imath}-\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}\right)</math></center>
Aplicando ahora la expresión para la velocidad del punto B
Aplicando ahora la expresión para la velocidad del punto B
Línea 52: Línea 52:
<center><math>\omega = 6\,</math>{{tose}}<math>\vec{\omega}=4\vec{\imath}-4\vec{\jmath}-2\vec{k}</math></center>
<center><math>\omega = 6\,</math>{{tose}}<math>\vec{\omega}=4\vec{\imath}-4\vec{\jmath}-2\vec{k}</math></center>
-
==Velocidad del punto C==
+
==Velocidad del punto P==
-
Una vez que tenemos la velocidad de un punto conocido y la velocidad angular del sólido, podemos hallar la velocidad de cualquier otro. Así, para el punto C
+
Una vez que tenemos la velocidad de un punto conocido y la velocidad angular del sólido, podemos hallar la velocidad de cualquier otro. Así, para el punto P
-
<center><math>\overrightarrow{AC}=\vec{\jmath}+\vec{k}</math> {{tose}}<math>\vec{v}^C = \overbrace{\vec{v}^A}^{=\vec{0}} + \vec{\omega}\times\overrightarrow{AC} = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 4 & -4 & -2\\ 0 & 1 & 1\end{matrix}\right|=-2\vec{\imath}-4\vec{\jmath}+4\vec{k}</math></center>
+
<center><math>\overrightarrow{AP}=\vec{\jmath}+\vec{k}</math> {{tose}}<math>\vec{v}^P = \overbrace{\vec{v}^A}^{=\vec{0}} + \vec{\omega}\times\overrightarrow{AP} = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 4 & -4 & -2\\ 0 & 1 & 1\end{matrix}\right|=-2\vec{\imath}-4\vec{\jmath}+4\vec{k}</math></center>
[[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]]
[[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]]
 +
[[Categoría:Problemas de cinemática del sólido rígido]]

última version al 09:37 24 sep 2015

Contenido

1 Enunciado

Un sólido rígido se encuentra en rotación instantánea alrededor de un eje que pasa por el punto A(1,0, − 1) y lleva la dirección del vector 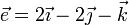\vec{e}=2\vec{\imath}-2\vec{\jmath}-\vec{k}, de tal forma que la velocidad del punto B(0,2,1) es

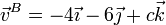
\vec{v}^B=-4\vec{\imath}-6\vec{\jmath}+c\vec{k}
  1. Halle el valor de la constante c.
  2. Calcule la velocidad angular instantánea.
  3. Calcule la velocidad del punto P(1,1,0).

Todas las cantidades están expresadas en las unidades del SI.

2 Valor de la constante

Por ser A un punto del eje instantáneo de rotación, EIR

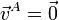
\vec{v}^A = \vec{0}

y la velocidad de cualquier otro punto, en particular B, verifica

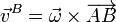
\vec{v}^B = \vec{\omega}\times\overrightarrow{AB}

Esto implica que la velocidad de B es perpendicular a la velocidad angular, lo que nos proporciona una ecuación para la constante

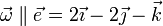
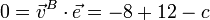
\vec{\omega}\parallel \vec{e}=2\vec{\imath}-2\vec{\jmath}-\vec{k}   \Rightarrow   0 = \vec{v}^B\cdot\vec{e}=-8+12-c   \Rightarrow   c=4\,

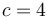
y resulta la velocidad para el punto B

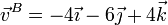
\vec{v}^B = -4\vec{\imath}-6\vec{\jmath}+4\vec{k}

3 Velocidad angular instantánea

Para hallar la velocidad angular, primero la escribimos como el producto de una componente escalar por el unitario en su dirección

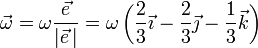
\vec{\omega} = \omega\frac{\vec{e}}{|\vec{e}\,|}=\omega\left(\frac{2}{3}\vec{\imath}-\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}\right)

Aplicando ahora la expresión para la velocidad del punto B

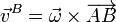
\vec{v}^B = \vec{\omega}\times\overrightarrow{AB}

siendo

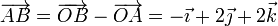
\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-\vec{\imath}+2\vec{\jmath}+2\vec{k}

lo que nos da

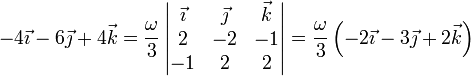
-4\vec{\imath}-6\vec{\jmath}+4\vec{k} = \frac{\omega}{3}\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 2 & -2 & -1\\ -1 & 2 & 2\end{matrix}\right|=\frac{\omega}{3}\left(-2\vec{\imath}-3\vec{\jmath}+2\vec{k}\right)

Igualando componente a componente

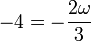
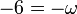
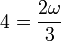
-4 = -\frac{2\omega}{3}        -6 = -\omega\,        4 = \frac{2\omega}{3}

Las tres ecuaciones conducen a la misma solución

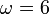
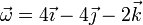
\omega = 6\,   \Rightarrow   \vec{\omega}=4\vec{\imath}-4\vec{\jmath}-2\vec{k}

4 Velocidad del punto P

Una vez que tenemos la velocidad de un punto conocido y la velocidad angular del sólido, podemos hallar la velocidad de cualquier otro. Así, para el punto P

\overrightarrow{AP}=\vec{\jmath}+\vec{k}    \Rightarrow   \vec{v}^P = \overbrace{\vec{v}^A}^{=\vec{0}} + \vec{\omega}\times\overrightarrow{AP} = \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 4 & -4 & -2\\ 0 & 1 & 1\end{matrix}\right|=-2\vec{\imath}-4\vec{\jmath}+4\vec{k}
Obtenido de "http://tesla.us.es/wiki/index.php/4.4._S%C3%B3lido_en_rotaci%C3%B3n_instant%C3%A1nea"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 09:37, 24 sep 2015. - Esta página ha sido visitada 8.883 veces. - Aviso legal - Acerca de Laplace