Test de la 2ª Convocatoria 2014-2015

De Laplace

(Diferencias entre revisiones)

Revisión de 14:23 10 sep 2015

1 Tres cargas alineadas

Se tienen tres cargas iguales $q$ situadas sobre el eje X en $x 1 = 0$ , $x 2 = 3 a$ y $x 3 = 4 a$

Archivo:Tres-cargas-alineadas.png.png

1.1 Pregunta 1

¿Cuál de las tres experimenta una fuerza más intensa?

A La 3.
B La 2.
C Las tres la misma
D La 1.

1.2 Pregunta 2

¿Cuál de las tres se encuentra a mayor potencial eléctrico debido a las otras dos?

A La 3.
B La 2.
C La 1.
D Las tres al mismo

2 Proceso adiabático

En un proceso adiabático de un sistema…

A la entropía del sistema siempre aumenta.
B la entropía del sistema siempre permanece constante.
C el trabajo que entra en el sistema es igual al que sale de él.
D el trabajo neto que entra es igual al aumento de la energía total.

3 Dos superficies cargadas

Se tiene un sistema formado por dos superficies esféricas cargadas uniformemente, tal como se ve en la figura.

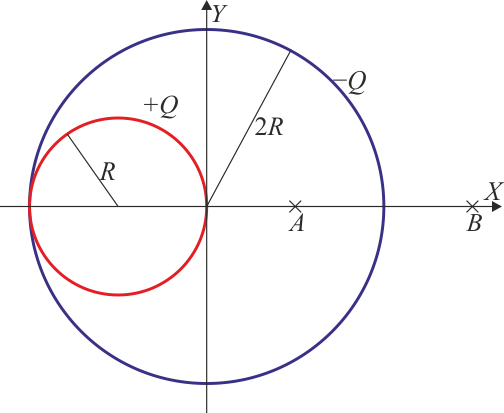
El campo eléctrico en cualquier punto del eje OX es de la forma

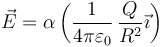
$\vec{E}=\alpha\left(\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{R^2}\vec{\imath}\right)$

con $α$ dependiente de la posición

3.1 Pregunta 1

¿Cuánto vale $α$ en el punto 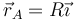$\vec{r}_A=R\vec{\imath}$ ?

A 1
B 0
C −3/4
D 1/4

3.2 Pregunta 2

¿Y en el punto 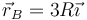$\vec{r}_B=3R\vec{\imath}$ ?

A −1/9
B −7/144
C −8/9
D 0

4 Calentamiento del ambiente

En un cilindro de paredes adiabáticas con un pistón móvil se encuentra una cierta cantidad de gas ideal. Inicialmente el pistón se encuentra aislado térmicamente y el gas se encuentra a la presión y temperatura del ambiente.

4.1 Pregunta 1

Si en estas condiciones se aumenta exclusivamente la temperatura del ambiente de manera gradual, el pistón…

A no se mueve y la presión del gas interior permanece constante.
B se mueve de forma que el gas se contrae.
C no se mueve pero la presión del gas interior aumenta.
D se mueve de forma que el gas se expande.

4.2 Pregunta 2

Si, sin modificar la nueva temperatura del ambiente, se retira el aislante térmico del pistón, éste…

A se mueve de forma que el gas se contrae.
B se mueve de forma que el gas se expande.
C no se mueve pero la presión del gas interior aumenta.
D no se mueve y la presión del gas interior permanece constante.

5 Dos hilos en paralelo

Se conectan en paralelo dos hilos de la misma longitud y la misma sección, uno de ellos es de cobre (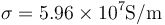 $\sigma=5.96\times 10^7\mathrm{S}/\mathrm{m}$ ) y el otro es de níquel ( 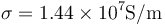$\sigma=1.44\times 10^7\mathrm{S}/\mathrm{m}$ ). Cuando la asociación se conecta a una diferencia de potencial $V 0$ …

A el campo eléctrico es mayor en el níquel.
B la densidad de corriente es mayor en el cobre.
C la densidad de corriente es la misma en los dos cables
D el campo eléctrico es mayor en el cobre.

6 Temperatura de una máquina térmica

Se quiere construir una máquina térmica tal que por cada $MW e$ de potencia generada, produzca solo 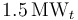$1.5\,\mathrm{MW}_t$ de calor de desecho al ambiente a 300K. Para que esta máquina funcione el foco caliente…

A debe estar como máximo a 900K
B debe estar como mínimo a 500K
C debe estar como máximo a 500K
D debe estar como mínimo a 900K

7 Espira en campo magnético

Una espira cuadrada con resistencia eléctrica $R$ y autoinducción despreciable se encuentra parcialmente inmersa en un campo magnético 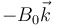$-B_0\vec{k}$ , tal como muestra la figura.

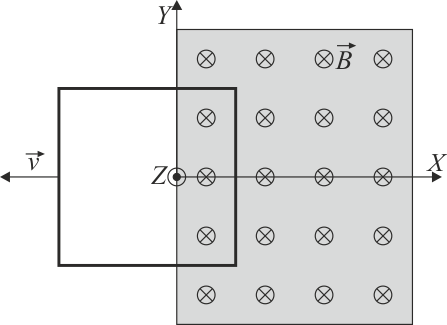
En un instante dado la espira se mueve con velocidad 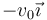$-v_0\vec{\imath}$ .

7.1 Pregunta 1

En este instante, por la espira…

A no circula corriente.
B circula una corriente en sentido horario.
C circula una corriente en sentido antihorario.
D puede circular corriente o no, dependiendo de la aceleración de la espira.

7.2 Pregunta 2

¿Cómo es la fuerza magnética sobre la espira en este instante?

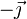
A En el sentido de $-\vec{\jmath}$
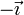
B En el sentido de $-\vec{\imath}$
C Nula.
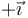
D En el sentido de $+\vec{\imath}$

8 Carga en campo magnético

Una carga puntual $q$ se mueve en el campo magnético

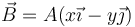
$\vec{B}=A(x\vec{\imath}-y\vec{\jmath})$

inicialmente se encuentra en el punto $P (b, b,0)$ moviéndose con velocidad 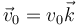$\vec{v}_0=v_0\vec{k}$

8.1 Pregunta 1

Cuando la partícula se mueve en este campo magnético, permanece constante…

A su posición.
B su energía cinética.
C su cantidad de movimiento.
D su velocidad.

8.2 Pregunta 2

¿Cuánto vale la fuerza sobre la partícula en $t = 0$ ?

A $\vec{F}=\vec{0}$
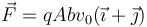
B $\vec{F}=qAbv_0(\vec{\imath}+\vec{\jmath})$
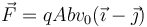
C $\vec{F}=qAbv_0(\vec{\imath}-\vec{\jmath})$
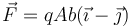
D $\vec{F}=qAb(\vec{\imath}-\vec{\jmath})$

9 Mezcla de agua y hielo

En un recipiente de paredes adiabáticas se ponen en contacto 400\,g de hielo a −10\,°C con 800\,g de agua a +10\,°C. El calor específico del agua es 4.18\,kJ/kg·K, el del hielo es 2.09\,kJ/kg·K y la entalpía específica de fusión 334\,kJ/kg. Una vez que se ha alcanzado el equilibrio térmico…

9.1 Pregunta 1

¿Cuál es la temperatura final del agua?

A 7.5\,°C
B 2.5\,°C
C 5.0\,°C
D 0.0\,°C

9.2 Pregunta 2

Al final del proceso, ¿cuánto hielo hay?

A 0\,g.
B 475\,g
C 400\,g
D 325\,g

10 Potencia disipada en una resistencia

Se conecta una resistencia externa $R$ a los polos de una fuente de tensión real, con f.e.m. 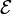$\mathcal{E}$ y resistencia interna $r$ . ¿Cuánto vale la potencia disipada en $R$ ?

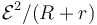
A $\mathcal{E}^2/(R+r)$
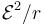
B $\mathcal{E}^2/r$
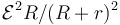
C $\mathcal{E}^2R/(R+r)^2$
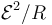
D $\mathcal{E}^2/R$

@@ Línea 1: / Línea 1: @@
 ==Tres cargas alineadas==
-Se tienen tres cargas iguales $q$ situadas sobre el eje X en $x_1=0$, $x_2=3a$ y $x_3=4a$
+Se tienen tres cargas iguales <math>q</math> situadas sobre el eje X en <math>x_1=0</math>, <math>x_2=3a</math> y <math>x_3=4a</math>
 <center>[[Archivo:tres-cargas-alineadas.png.png]]</center>
@@ Línea 37: / Línea 37: @@
 <center><math>\vec{E}=\alpha\left(\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{R^2}\vec{\imath}\right)</math></center>
-con $\alpha$ dependiente de la posición
+con <math>\alpha</math> dependiente de la posición
 ===Pregunta 1===
-¿Cuánto vale $\alpha$ en el punto  $\vec{r}_A=R\vec{\imath}$?
+¿Cuánto vale <math>\alpha</math> en el punto  <math>\vec{r}_A=R\vec{\imath}</math>?
 :* '''A''' 1
@@ Línea 48: / Línea 48: @@
 ===Pregunta 2===
-¿Y en el punto $\vec{r}_B=3R\vec{\imath}$?
+¿Y en el punto <math>\vec{r}_B=3R\vec{\imath}</math>?
 :* '''A''' &minus;1/9
@@ Línea 75: / Línea 75: @@
 ==Dos hilos en paralelo==
-Se conectan en paralelo dos hilos de la misma longitud y la misma sección, uno de ellos es de cobre ($\sigma=5.96\times 10^7\mathrm{S}/\mathrm{m}$) y el otro es de níquel ($\sigma=1.44\times 10^7\mathrm{S}/\mathrm{m}$). Cuando la asociación se conecta a una diferencia de potencial $V_0$&hellip;
+Se conectan en paralelo dos hilos de la misma longitud y la misma sección, uno de ellos es de cobre (<math>\sigma=5.96\times 10^7\mathrm{S}/\mathrm{m}</math>) y el otro es de níquel (<math>\sigma=1.44\times 10^7\mathrm{S}/\mathrm{m}</math>). Cuando la asociación se conecta a una diferencia de potencial <math>V_0</math>&hellip;
 :* '''A''' el campo eléctrico es mayor en el níquel.
@@ Línea 83: / Línea 83: @@
 ==Temperatura de una máquina térmica==
-Se quiere construir una máquina térmica tal que por cada $\mathrm{MW}_e$ de potencia generada, produzca solo $1.5\,\mathrm{MW}_t$ de calor de desecho al ambiente a 300K. Para que esta máquina funcione el foco caliente&hellip;
+Se quiere construir una máquina térmica tal que por cada <math>\mathrm{MW}_e</math> de potencia generada, produzca solo <math>1.5\,\mathrm{MW}_t</math> de calor de desecho al ambiente a 300K. Para que esta máquina funcione el foco caliente&hellip;
 :* '''A''' debe estar como máximo a 900K
@@ Línea 91: / Línea 91: @@
 ==Espira en campo magnético==
-Una espira cuadrada con resistencia eléctrica $R$ y autoinducción despreciable se encuentra parcialmente inmersa en un campo magnético $-B_0\vec{k}$, tal como muestra la figura.
+Una espira cuadrada con resistencia eléctrica <math>R</math> y autoinducción despreciable se encuentra parcialmente inmersa en un campo magnético <math>-B_0\vec{k}</math>, tal como muestra la figura.
 <center>[[Archivo:espira-saliente.png]]</center>
-En un instante dado la espira se mueve con velocidad $-v_0\vec{\imath}$.
+En un instante dado la espira se mueve con velocidad <math>-v_0\vec{\imath}</math>.
 ===Pregunta 1===
@@ Línea 108: / Línea 108: @@
 ¿Cómo es la fuerza magnética sobre la espira en este instante?
-:* '''A''' En el sentido de $-\vec{\jmath}$
+:* '''A''' En el sentido de <math>-\vec{\jmath}</math>
-:* '''B''' En el sentido de $-\vec{\imath}$
+:* '''B''' En el sentido de <math>-\vec{\imath}</math>
 :* '''C''' Nula.
-:* '''D''' En el sentido de $+\vec{\imath}$
+:* '''D''' En el sentido de <math>+\vec{\imath}</math>
 ==Carga en campo magnético==
-Una carga puntual $q$ se mueve en el campo magnético
+Una carga puntual <math>q</math> se mueve en el campo magnético
 <center><math>\vec{B}=A(x\vec{\imath}-y\vec{\jmath})</math></center>
-inicialmente se encuentra en el punto $P(b,b,0)$ moviéndose con velocidad $\vec{v}_0=v_0\vec{k}$
+inicialmente se encuentra en el punto <math>P(b,b,0)</math> moviéndose con velocidad <math>\vec{v}_0=v_0\vec{k}</math>
 ===Pregunta 1===
@@ Línea 129: / Línea 129: @@
 ===Pregunta 2===
-¿Cuánto vale la fuerza sobre la partícula en $t=0$?
+¿Cuánto vale la fuerza sobre la partícula en <math>t=0</math>?
-:* '''A''' $\vec{F}=\vec{0}$
+:* '''A''' <math>\vec{F}=\vec{0}</math>
-:* '''B''' $\vec{F}=qAbv_0(\vec{\imath}+\vec{\jmath})$
+:* '''B''' <math>\vec{F}=qAbv_0(\vec{\imath}+\vec{\jmath})</math>
-:* '''C''' $\vec{F}=qAbv_0(\vec{\imath}-\vec{\jmath})$
+:* '''C''' <math>\vec{F}=qAbv_0(\vec{\imath}-\vec{\jmath})</math>
-:* '''D''' $\vec{F}=qAb(\vec{\imath}-\vec{\jmath})$
+:* '''D''' <math>\vec{F}=qAb(\vec{\imath}-\vec{\jmath})</math>
 ==Mezcla de agua y hielo==
@@ Línea 156: / Línea 156: @@
 ==Potencia disipada en una resistencia==
-Se conecta una resistencia externa $R$ a los polos de una fuente de tensión real, con f.e.m. $\mathcal{E}$ y resistencia interna $r$. ¿Cuánto vale la potencia disipada en $R$?
+Se conecta una resistencia externa <math>R</math> a los polos de una fuente de tensión real, con f.e.m. <math>\mathcal{E}</math> y resistencia interna <math>r</math>. ¿Cuánto vale la potencia disipada en <math>R</math>?
-:* '''A''' $\mathcal{E}^2/(R+r)$
+:* '''A''' <math>\mathcal{E}^2/(R+r)</math>
-:* '''B''' $\mathcal{E}^2/r$
+:* '''B''' <math>\mathcal{E}^2/r</math>
-:* '''C''' $\mathcal{E}^2R/(R+r)^2$
+:* '''C''' <math>\mathcal{E}^2R/(R+r)^2</math>
-:* '''D''' $\mathcal{E}^2/R$
+:* '''D''' <math>\mathcal{E}^2/R</math>