Preguntas de test de inducción electromagnética (GIE)
De Laplace
(→Comparación de bobinas) |
|||
| Línea 22: | Línea 22: | ||
! D | ! D | ||
|} | |} | ||
| - | + | ;Solución: | |
La respuesta correcta es la '''<span style="color:red;">D<span>'''. | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
| Línea 46: | Línea 46: | ||
:*'''C''' Una de 500 vueltas, 30 cm de longitud y 2 cm de diámetro. | :*'''C''' Una de 500 vueltas, 30 cm de longitud y 2 cm de diámetro. | ||
:*'''D''' Una de 400 vueltas, 20 cm de longitud y 1 cm de diámetro. | :*'''D''' Una de 400 vueltas, 20 cm de longitud y 1 cm de diámetro. | ||
| - | + | ;Solución: | |
La respuesta correcta es la '''<span style="color:red;">C<span>'''. | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| Línea 74: | Línea 74: | ||
:*'''C''' Aumenta linealmente con el tiempo. | :*'''C''' Aumenta linealmente con el tiempo. | ||
:*'''D''' Aumenta cuadráticamente con el tiempo. | :*'''D''' Aumenta cuadráticamente con el tiempo. | ||
| - | + | ;Solución: | |
La respuesta correcta es la '''<span style="color:red;">C<span>'''. | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| Línea 97: | Línea 97: | ||
:*'''C''' Aumenta linealmente con el tiempo. | :*'''C''' Aumenta linealmente con el tiempo. | ||
:*'''D''' Aumenta cuadráticamente con el tiempo. | :*'''D''' Aumenta cuadráticamente con el tiempo. | ||
| - | + | ;Solución: | |
La respuesta correcta es la '''<span style="color:red;">D<span>'''. | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
| Línea 127: | Línea 127: | ||
:*'''C''' En <math>t = 10\,\mathrm{s}</math> | :*'''C''' En <math>t = 10\,\mathrm{s}</math> | ||
:*'''D''' En <math>t = 6\,\mathrm{s}</math> | :*'''D''' En <math>t = 6\,\mathrm{s}</math> | ||
| - | + | ;Solución: | |
La respuesta correcta es la '''<span style="color:red;">D<span>'''. | La respuesta correcta es la '''<span style="color:red;">D<span>'''. | ||
Revisión de 08:03 14 jun 2015
Contenido |
1 Corriente inducida en una espira
Una espira circular de radio b, resistencia R y autoinducción despreciable, situada en el plano XY, se encuentra sumergida en un campo magnético uniforme que varía en el tiempo como un pulso gaussiano
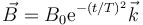
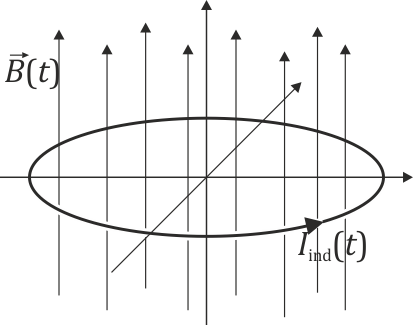
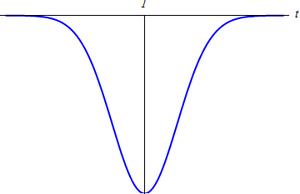
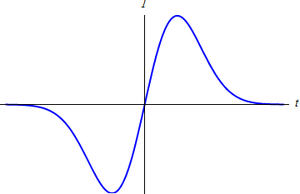
¿Cuál de las siguientes cuatro figuras describe correctamente la corriente que circula por la espira, considerada en sentido antihorario alrededor del eje Z?

| 
|
| A | B |
|---|---|
| 
|
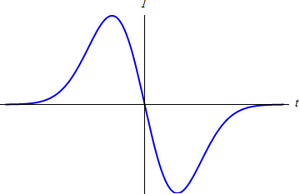
| C | D |
- Solución
La respuesta correcta es la D.
De acuerdo con la ley de Faraday, la corriente inducida en la espira cumple
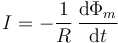
Puesto que en este caso el campo es uniforme, este flujo es igual al producto del campo por el área S del círculo, lo que nos deja con

Es decir, no están preguntando por la derivada de B respecto al tiempo, cambiada de signo.
Por las propiedades de las derivadas, esto quiere decir que I será negativa cuando B crece y positiva cuando B decrece (de acuerdo con al ley de Lenz).
Por tanto, la respuesta correcta es la D.
2 Comparación de bobinas
¿Cuál de las siguientes bobinas tiene un mayor coeficiente de autoinducción?
- A Una de 300 vueltas, 15 cm de longitud y 2 cm de diámetro.
- B Una de 200 vueltas, 8 cm de longitud y 1 cm de diámetro.
- C Una de 500 vueltas, 30 cm de longitud y 2 cm de diámetro.
- D Una de 400 vueltas, 20 cm de longitud y 1 cm de diámetro.
- Solución
La respuesta correcta es la C.
El coeficiente de autoinducción de un solenoide largo viene dado por la expresión
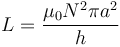
En este caso, puesto que μ0 y π son los mismos para todos, se trata de comparar el cociente N2a2 / h, lo que da
- A: 300²×2²/15 = 24000
- B: 200²×1²/8 = 5000
- C: 500²×2²/30 = 33333
- D: 400²×1²/20 = 8000
En realidad, hemos hecho la comparación empleando el diámetro, en vez del radio, pero eso no afecta al resultado, ya que solo produce un factor 4, en todos los casos, que no importa a la hora de ver cuál es más grande.
3 Espira en forma de escuadra
Una espira en forma de escuadra con resistencia R y autoinducción despreciable penetra en un campo magnético uniforme con una velocidad paralela a uno de sus catetos.
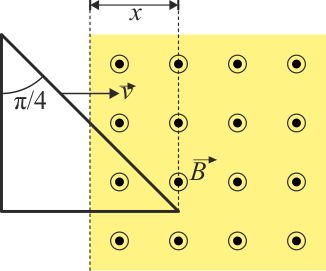
3.1 Pregunta 1
Si la velocidad de la espira es constante, ¿cómo es la corriente que se induce en ella mientras va entrando?
- A Tiende exponencialmente a un valor constante
- B Permanece constante.
- C Aumenta linealmente con el tiempo.
- D Aumenta cuadráticamente con el tiempo.
- Solución
La respuesta correcta es la C.
La corriente que circula por la espira se obtiene a partir de la fuerza electromotriz inducida
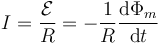
Puesto que el campo magnético es uniforme, el flujo magnético es proporcional al área del triángulo que está dentro del campo
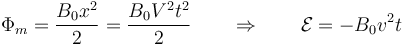
Por tanto la intensidad de corriente aumenta linealmente con el tiempo.
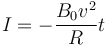
siendo su sentido el horario (dado por el signo negativo).
3.2 Pregunta 2
¿Y la fuerza magnética sobre la espira?
- A Permanece constante.
- B Tiende exponencialmente a un valor constante
- C Aumenta linealmente con el tiempo.
- D Aumenta cuadráticamente con el tiempo.
- Solución
La respuesta correcta es la D.
Una espira que se encuentra [Fuerzas_magnéticas_(GIE)#Espira_sumergida_parcialmente_en_un_campo|parcialmente sumergida] en un campo uniforme experimenta una fuerza
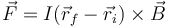
En este caso
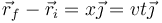
por lo que la fuerza magnética es igual a
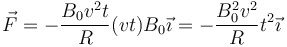
Lo relevante para responder a la pregunta es que la intensidad de corriente aumenta linealmente con el tiempo y la distancia entre los puntos de entrada y salida también lo hace, por lo que su producto aumenta cuadráticamente con el tiempo.
4 Flujo magnético variable
La figura representa el flujo magnético a través de una espira de
resistencia 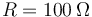 y autoinducción despreciable, como función del tiempo.
y autoinducción despreciable, como función del tiempo.

¿En cuál de los siguientes instantes es mayor, en valor absoluto, la corriente que circula por la espira?
- A En
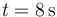
- B En
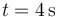
- C En

- D En

- A En
- Solución
La respuesta correcta es la D.
Puesto que la intensidad de corriente en la espira es igual a
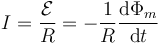
lo que se está pidiendo realmente es en qué instante es mayor la derivada, es decir, la pendiente de la gráfica, lo cual ocurre en t = 6s.





