Fuerza magnética sobre una espira cuadrada
De Laplace
| Línea 16: | Línea 16: | ||
Para este problema tenemos varios casos dependiendo de la relación entre <math>a</math> y <math>b</math> | Para este problema tenemos varios casos dependiendo de la relación entre <math>a</math> y <math>b</math> | ||
| - | ==Caso b | + | ==Caso b ≥ a== |
| - | En el primer caso la solución es trivial. la espira está completamente fuera del campo magnético y la fuerza sobre cada lada es nula | + | En el primer caso la solución es trivial. la espira está completamente fuera del campo magnético y la fuerza sobre cada lada es nula. |
<center><math>\vec{F}_1=\vec{F}_2=\vec{F}_3=\vec{F}_4=\vec{0}</math></center> | <center><math>\vec{F}_1=\vec{F}_2=\vec{F}_3=\vec{F}_4=\vec{0}</math></center> | ||
| Línea 24: | Línea 24: | ||
<center><math>\vec{F}=\sum_i\vec{F}_i=\vec{0}</math></center> | <center><math>\vec{F}=\sum_i\vec{F}_i=\vec{0}</math></center> | ||
| - | ==Caso 0 < b < a== | + | |
| + | ==Caso 0 ≤ b ≤ a== | ||
| + | En el segundo caso, tenemos dos lados (1 y 4, si los etiquetamos según el cuadrante) parcialmente inmersos en el campo magnético y otros dos (2 y 3) completamente fuera de él. | ||
| + | |||
| + | <center><math>\vec{F}_2=\vec{F}_3 =\vec{0}</math></center> | ||
| + | |||
| + | Para el lado 1, el tramo que está dentro del campo magnético es | ||
| + | |||
| + | <center><math>\overrightarrow{PQ}_1 = (a-b)\left(-\vec{\imath}+\vec{\jmath})</math></center> | ||
| + | |||
| + | por lo que la fuerza sobre este lado vale | ||
| + | |||
| + | <center><math>\vec{F}_1=I(a-b)\left(-\vec{\imath}+\vec{\jmath})\times(B_0\vec{k})=I(a-b)B_0\left(\vec{\imath}+\vec{\jmath})</math></center> | ||
| + | |||
| + | Para el lado 4 | ||
| + | |||
| + | <center><math>\overrightarrow{PQ}_4 = (a-b)\left(\vec{\imath}+\vec{\jmath})</math></center> | ||
| + | |||
| + | y queda | ||
| + | |||
| + | <center><math>\vec{F}_4=I(a-b)\left(\vec{\imath}+\vec{\jmath})\times(B_0\vec{k})=I(a-b)B_0\left(\vec{\imath}-\vec{\jmath})</math></center> | ||
| + | |||
| + | Sumando estas dos obtenemos la fuerza neta | ||
| + | |||
| + | <center><math>\vec{F}=2I(a-b)B_0\vec{\imath}</math></center> | ||
| + | |||
| + | A esta misma fuerza neta se llega considerando el punto inicial y final de todo el tramo | ||
| + | |||
| + | <center><math>\vec{F}=I\overrightarrow{P_4Q_1}\times\vec{B}=I\left(2(a-b)\vec{\jmath}\right)\times(B_0\vec{k})=2I(a-b)B_0\vec{\imath}</math></center> | ||
| + | |||
| + | Este caso incluye el caso particular en que b=0, es decir, la espira entra hasta la mitad en el campo magnético | ||
| + | |||
| + | <center><math>(b=0)\qquad\qquad \vec{F}_1=IaB_0\left(\vec{\imath}+\vec{\jmath})\qquad\vec{F}_4=IaB_0\left(\vec{\imath}-\vec{\jmath})\qquad\vec{F}=2IaB_0\vec{\imath}</math></center> | ||
| + | |||
| + | |||
==Caso -a < b < 0== | ==Caso -a < b < 0== | ||
==Caso b < -a== | ==Caso b < -a== | ||
[[Categoría:Problemas de campo magnético (GIE)]] | [[Categoría:Problemas de campo magnético (GIE)]] | ||
Revisión de 15:47 12 jun 2015
Contenido |
1 Enunciado
El campo entre los polos de un imán se puede modelar como un campo magnético uniforme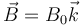 
en el semiespacio
x > b. Una espira cuadrada se encuentra sumergida parcialmente en este campo. La espira se encuentra en el plano XY, girada 45° respecto a los ejes, de forma que sus vértices se hallan en 
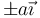y en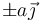 
. Por la espira circula una intensidad de corriente I. Calcule la fuerza sobre cada lado de la espira como función de lo que penetra la espira en el campo y la fuerza neta (distínganse los casos necesarios).
2 Introducción
La fuerza sobre un hilo inmerso en un campo magnético viene dada por la integral
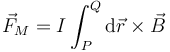
siendo P el punto donde comienza el hilo y Q donde acaba. En el caso de un campo magnético uniforme, 
sale de la integral y queda
Obsérvese que esta fórmula no depende de que el hilo sea recto o curvado.
Para este problema tenemos varios casos dependiendo de la relación entre a y b
3 Caso b ≥ a
En el primer caso la solución es trivial. la espira está completamente fuera del campo magnético y la fuerza sobre cada lada es nula.
y lógicamente también lo es la fuerza neta
4 Caso 0 ≤ b ≤ a
En el segundo caso, tenemos dos lados (1 y 4, si los etiquetamos según el cuadrante) parcialmente inmersos en el campo magnético y otros dos (2 y 3) completamente fuera de él.
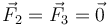
Para el lado 1, el tramo que está dentro del campo magnético es
por lo que la fuerza sobre este lado vale
Para el lado 4
y queda
Sumando estas dos obtenemos la fuerza neta
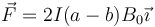
A esta misma fuerza neta se llega considerando el punto inicial y final de todo el tramo
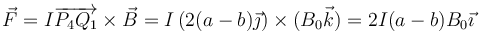
Este caso incluye el caso particular en que b=0, es decir, la espira entra hasta la mitad en el campo magnético
