Dipolo eléctrico (GIE)
De Laplace
| Línea 8: | Línea 8: | ||
<center><math>\vec{p}=q\,\Delta\vec{r}</math></center> | <center><math>\vec{p}=q\,\Delta\vec{r}</math></center> | ||
| - | siendo <math>\Delta\vec{r}</math> el vector de posición | + | siendo <math>\Delta\vec{r}</math> el vector de posición relativa que va de la carga negativa a la positiva. |
| - | Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale | + | Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale a |
| - | <center><math>\vec{p}=q(\vec{r}_+-\vec{r}_-)=q_+\vec{r}_++q_\vec{r}_-</math></center> | + | <center><math>\vec{p}=q(\vec{r}_{+}-\vec{r}_{-})=q_{+}\vec{r}_{+}+q_\vec{r}_{-}</math></center> |
Y de aquí pasamos a una distribución de cargas puntuales | Y de aquí pasamos a una distribución de cargas puntuales | ||
Revisión de 18:46 20 mar 2015
1 Definición. Momento dipolar
En su versión más sencilla, un dipolo es un sistema formado por dos cargas de la misma magnitud y signo opuesto, separadas una cierta distancia.
Más en general, un sistema neutro pero en el que el centro de las cargas positivas no coincide con el de las negativas también se conoce como un dipolo. Un ejemplo típico es la molécula de agua. Al ser el oxígeno más electronegativo que el hidrógeno, se produce una acumulación de carga negativa en el lado en que se halla el oxígeno, y de carga positiva en el opuesto.
El dipolo se caracteriza matemáticamente por su momento dipolar, que para dos cargas puntuales se define como
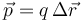
siendo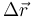 
el vector de posición relativa que va de la carga negativa a la positiva.
Esta expresión se generaliza fácilmente a una distribución arbitraria observando que equivale a
Y de aquí pasamos a una distribución de cargas puntuales
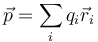
y a una dustribución volumétrica, superficial o lineal
