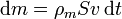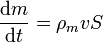Flujo de un campo vectorial
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Introducción== ==Flujo de un campo uniforme en una sección ortogonal== ==Flujo de un campo uniforme en una sección oblicua== ==Flujo de un campo a través de una superficie arbit...) |
(→Flujo de un campo uniforme en una sección ortogonal) |
||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
==Flujo de un campo uniforme en una sección ortogonal== | ==Flujo de un campo uniforme en una sección ortogonal== | ||
| + | Consideremos en primer lugar el caso de una tubería de sección <math>S</math> por la cual fluye agua con la misma velocidad <math>v</math> en todos sus puntos. Nos preguntamos por el caudal de la tubería, esto es, por la cantidad de agua que atraviesa una sección de la tubería en la unidad de tiempo. En un intervalo \mathrm{d}t la cantidad de aqua que atraviesa S es aquella que se encuentra a una distancia menor de <math>v\,\mathrm{d}t</math>. | ||
| + | |||
| + | <math>\mathrm{d}m = \rho_m S v\,\mathrm{d}t</math>{{tose}} <math>\frac{\mathrm{d}m}{\mathrm{d}t} = \rho_mvS</math> | ||
| + | |||
==Flujo de un campo uniforme en una sección oblicua== | ==Flujo de un campo uniforme en una sección oblicua== | ||
==Flujo de un campo a través de una superficie arbitrarios== | ==Flujo de un campo a través de una superficie arbitrarios== | ||
==Flujo a través de una superficie cerrada== | ==Flujo a través de una superficie cerrada== | ||
[[Categoría:Fundamentos matemáticos]] | [[Categoría:Fundamentos matemáticos]] | ||
Revisión de 16:22 27 dic 2008
Contenido |
1 Introducción
2 Flujo de un campo uniforme en una sección ortogonal
Consideremos en primer lugar el caso de una tubería de sección S por la cual fluye agua con la misma velocidad v en todos sus puntos. Nos preguntamos por el caudal de la tubería, esto es, por la cantidad de agua que atraviesa una sección de la tubería en la unidad de tiempo. En un intervalo \mathrm{d}t la cantidad de aqua que atraviesa S es aquella que se encuentra a una distancia menor de 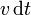 .
.