Potencial eléctrico debido a una esfera maciza
De Laplace
| Línea 24: | Línea 24: | ||
<center><math>\mathrm{d}\vec{r}=\mathrm{d}r\,\vec{u}_r</math></center> | <center><math>\mathrm{d}\vec{r}=\mathrm{d}r\,\vec{u}_r</math></center> | ||
| - | Este camino discurre completamente por exterior de la esfera. Por tanto, en todos los puntos por los que pasa el campo tiene la expresión | + | Este camino discurre completamente por exterior de la esfera. |
| + | |||
| + | <center>[[Archivo:integral-exterior-esfera.png]]</center> | ||
| + | |||
| + | Por tanto, en todos los puntos por los que pasa el campo tiene la expresión | ||
<center><math>\vec{E}=\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r</math></center> | <center><math>\vec{E}=\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r</math></center> | ||
| Línea 37: | Línea 41: | ||
Este potencial es idéntico al de una carga puntual, lo cual es lógico, ya que si es el campo exterior es equivalente al de una carga su integral también lo será. | Este potencial es idéntico al de una carga puntual, lo cual es lógico, ya que si es el campo exterior es equivalente al de una carga su integral también lo será. | ||
| + | |||
| + | ===Interior de la esfera=== | ||
| + | Como en el problema de la [[Potencial_eléctrico_debido_a_una_superficie_esférica#En_un_punto_del_interior|esfera hueca]] para los puntos del interior hay que tener cuidado con el que el origen de potencial se halle en el infinito. | ||
| + | |||
| + | Esto quiere decir que para llegar al punto de destino hay que recorrer un tramo por el exterior y otro por el interior de la esfera. | ||
| + | |||
| + | |||
| + | <center>[[Archivo:integral-interior-esfera.png]]</center> | ||
| + | |||
| + | Considerando un camino rectilíneo, dividimos la integral en dos partes, una hasta el punto B en que toca a la esfera y otra desde ahí hasta A | ||
| + | |||
| + | <center><math>V_A = -\int_O^A\vec{E}\cdot\mathrm{d}\vec{r}=-\int_O^B\vec{E}\cdot\mathrm{d}\vec{r}-\int_B^A\vec{E}\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | Sustituyendo la expresión del campo en cada región queda | ||
| + | |||
| + | <center><math>V(r) = -\int_\infty^R\frac{Q}{4\pi\varepsilon_0r^2}\cdot\mathrm{d}r-\int_R^r\frac{1}{3\varepsilon_0}\rho r\,\mathrm{d}r = \frac{Q}{4\pi\varepsilon_0R}-\frac{\rho_0}{3\varepsilon_0}\left(\frac{r^2}{2}-\frac{R^2}{2}\right)</math></center> | ||
| + | |||
| + | Sustituimos el valor de la densidad de carga | ||
| + | |||
| + | <center><math>\rho_0=\frac{Q}{4\pi R^3/3}=\frac{3Q}{4\pi R^3}</math></center> | ||
| + | |||
| + | y queda | ||
| + | |||
| + | <center><math>V(r) = \frac{Q}{4\pi\varepsilon_0R}+\frac{Q(R^2-r^2)}{8\pi\varepsilon_0R^3} = \frac{Q(3R^2-r^2)}{8\pi\varepsilon_0R^3}</math></center> | ||
| + | |||
| + | ===Potencial en cualquier punto del espacio=== | ||
| + | Reunimos los dos resultados y queda la expresión general | ||
| + | |||
| + | |||
| + | <center><math>V(r) = \left\{\begin{cases} \dfrac{Q(3R^2-r^2)}{8\pi\varepsilon_0R^3} & r < R \\ & \\ \dfrac{Q}{4\pi\varepsilon_0 r} & r \geq R\end{cases}\righ.</math></center> | ||
==Potencial en el centro de la esfera== | ==Potencial en el centro de la esfera== | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 23:06 6 mar 2015
Contenido |
1 Enunciado
Halle, a partir del campo eléctrico, el potencial eléctrico debido a una esfera de radio R que almacena una carga Q distribuida uniformemente en su volumen.
Para el centro de la esfera, calcule el potencial eléctrico por integración directa. Compruebe que el resultado coincide con el interior para este punto.
2 Potencial en cualquier punto
Tal como se ve en el problema “Campo de distribuciones con simetría esférica” el campo producido por una carga Q distribuida uniformemente en un volumen esférico es, escrito en su forma más usual
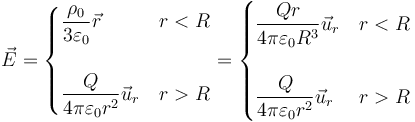
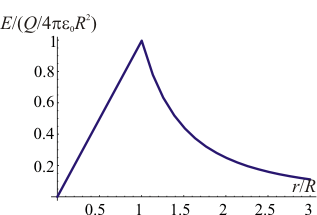
Las dos pueden escribirse en términos de la carga total o de la densidad de carga sin más que sustituir el que la densidad de carga es igual a la carga total dividida por el volumen en que está distribuida
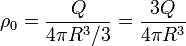
Para hallar el potencial eléctrico en cualquier punto del espacio debemos integrar este campo desde el infinito (origen de potencial) hasta el punto donde queremos conocerlo. Tenemos dos casos:
2.1 Exterior de la esfera
Esta parte del problema es idéntica al cálculo del potencial para una carga puntual y para una esfera hueca.
Tomamos un camino recto radial desde el infinito hasta una distancia r > R. Por ser radial, el diferencial de camino va en la dirección de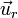 
y mide lo que cambie la distancia al centro de la esfera:
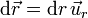
Este camino discurre completamente por exterior de la esfera.
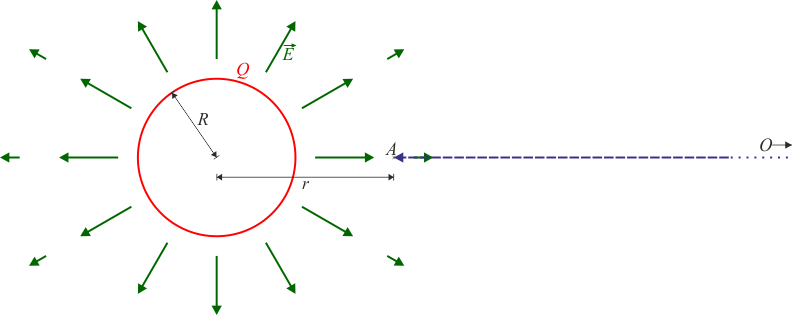
Por tanto, en todos los puntos por los que pasa el campo tiene la expresión
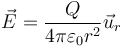
Nos queda el producto escalar
y la integral
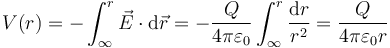
Este potencial es idéntico al de una carga puntual, lo cual es lógico, ya que si es el campo exterior es equivalente al de una carga su integral también lo será.
2.2 Interior de la esfera
Como en el problema de la esfera hueca para los puntos del interior hay que tener cuidado con el que el origen de potencial se halle en el infinito.
Esto quiere decir que para llegar al punto de destino hay que recorrer un tramo por el exterior y otro por el interior de la esfera.
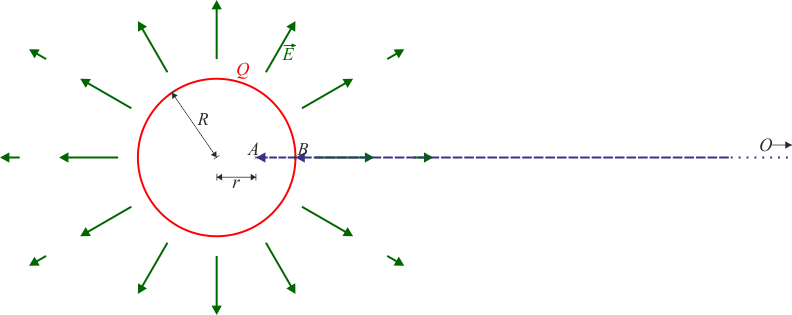
Considerando un camino rectilíneo, dividimos la integral en dos partes, una hasta el punto B en que toca a la esfera y otra desde ahí hasta A
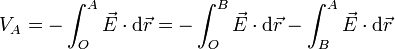
Sustituyendo la expresión del campo en cada región queda
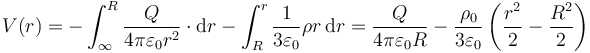
Sustituimos el valor de la densidad de carga
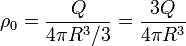
y queda
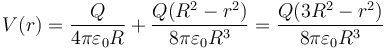
2.3 Potencial en cualquier punto del espacio
Reunimos los dos resultados y queda la expresión general
