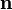Vector superficie

De Laplace

(Diferencias entre revisiones)

Revisión de 13:43 25 dic 2008

Contenido

1 Enunciado
2 Solución

1 Enunciado

Demuestre que integrando alrededor de una curva cerrada, $Γ$ , del plano $X Y$ , se cumple que

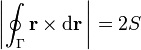
$\left| \oint_{\Gamma} \mathbf{r} \times \mathrm{d}\mathbf{r}\,\right| = 2 S$

donde 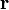$\mathbf{r}$ es el vector de posición y $S$ el área encerrada por $Γ$ .

A partir de aquí, deduzca que para una curva arbitraria en el espacio

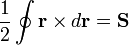
$\frac{1}{2}\oint\mathbf{r} \times d\mathbf{r}= \mathbf{S}$

donde 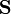$\mathbf{S}$ es un vector cuyas componentes son las áreas de las proyecciones de la curva sobre los planos coordenados.

2 Solución

2.1 caso de una curva plana

Supongamos, en primer lugar, que tenemos una curva plana, sobre la que situamos el plano $X Y$ . En este plano

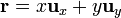
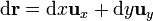
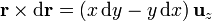
$\mathbf{r}=x\mathbf{u}_x+y\mathbf{u}_y$ $\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{u}_x+\mathrm{d}y\mathbf{u}_y$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)\mathbf{u}_z$

El módulo de la integral es por tanto igual a

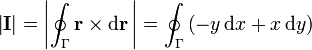
$\left|\mathbf{I}\right| = \left| \oint_{\Gamma} \mathbf{r} \times \mathrm{d}\mathbf{r}\,\right|=\oint_\Gamma \left(-y\,\mathrm{d}x+x\,\mathrm{d}y\right)$

Esta integral puede escribirse como una circulación

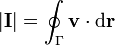
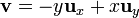
$\left|\mathbf{I}\right| = \oint_\Gamma \mathbf{v}\cdot\mathrm{d}\mathbf{r}$ $\mathbf{v}=-y\mathbf{u}_x+x\mathbf{u}_y$

Podemos entonces aplicar el teorema de Stokes

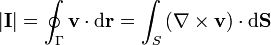
$\left|\mathbf{I}\right| = \oint_\Gamma \mathbf{v}\cdot\mathrm{d}\mathbf{r} = \int_S\left(\nabla\times\mathbf{v}\right)\cdot\mathrm{d}\mathbf{S}$

siendo el rotacional

$\nabla\times\mathbf{v} = \left|\begin{matrix}\mathbf{u}_x & \mathbf{u}_x & \mathbf{u}_x \\ & & \\ \displaystyle\frac{\partial\ }{\partial x} &\displaystyle\frac{\partial\ }{\partial y} & \displaystyle\frac{\partial\ }{\partial z} \\ & & \\ -y & x & 0\end{matrix}\right| = 2\mathbf{u}_z$

y el diferencial de seuperficie, por estar ésta en el plano XY

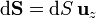
$\mathrm{d}\mathbf{S} = \mathrm{d}S\,\mathbf{u}_z$

con lo que queda finalmente

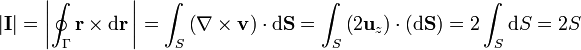
$\left|\mathbf{I}\right| = \left| \oint_{\Gamma} \mathbf{r} \times \mathrm{d}\mathbf{r}\,\right|= \int_S\left(\nabla\times\mathbf{v}\right)\cdot\mathrm{d}\mathbf{S}= \int_S\left(2\mathbf{u}_z\right)\cdot\left(\mathrm{d}\mathbf{S}\right) = 2\int_S \mathrm{d}S = 2S$

2.1.1 Interpretación geométrica

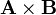Este resultado se puede obtener de forma sencilla usando exclusivamente álgebra vectorial. Dados dos vectores $\mathbf{A}$ y $\mathbf{B}$ , su producto vectorial $\mathbf{A}\times\mathbf{B}$ es un vector ortogonal a ambos y cuyo módulo es el área del paralelogramo definido por ambos vectores. El vector

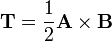
$\mathbf{T}=\frac{1}{2}\mathbf{A}\times\mathbf{B}$

será por tanto un vector ortogonal a ambos y con módulo el área de un triángulo definido por estos dos vectores.

Si consideramos el vector diferencial

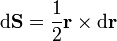
$\mathrm{d}\mathbf{S}=\frac{1}{2}\mathbf{r}\times\mathrm{d}\mathbf{r}$

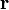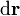obtendremos un vector de módulo el diferencial de área triangular, y por dirección la normal al plano definido por $\mathbf{r}$ y $\mathrm{d}\mathbf{r}$ . Para el caso de una curva contenida en el plano $z = 0$ esta dirección es constante y dada por $\mathbf{u}_z$ .

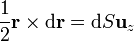
$\frac{1}{2}\mathbf{r}\times\mathrm{d}\mathbf{r}=\mathrm{d}S\mathbf{u}_z$

Integrando sobre una curva cerrada sumamos las áreas de todos los triángulos diferenciales, resultando el área total

$\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r}=\int_S \mathrm{d}S\mathbf{u}_z = S\mathbf{u}_z$

2.2 Caso de una curva alabeada

Supongamos ahora que tenemos una curva alabeada, esto es, que no puede contenerse en un plno, o una curva plana pero que no está situada en ninguno de los planos coordenados.

En esta curva tridimensional, tanto el vector de posición como el diferencial de camino poseen las tres componentes

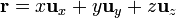
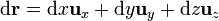
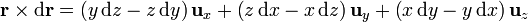
$\mathbf{r}=x\mathbf{u}_x+y\mathbf{u}_y+z\mathbf{u}_z$ $\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{u}_x+\mathrm{d}y\mathbf{u}_y+\mathrm{d}z\mathbf{u}_z$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=\left(y\,\mathrm{d}z-z\,\mathrm{d}y\right)\mathbf{u}_x+\left(z\,\mathrm{d}x-x\,\mathrm{d}z\right)\mathbf{u}_y+\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)\mathbf{u}_z$

Al sustituir en la integral nos resulta la suma de tres términos

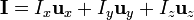
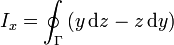
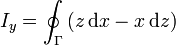
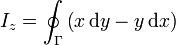
$\mathbf{I}=I_x\mathbf{u}_x+I_y\mathbf{u}_y+I_z\mathbf{u}_z$ $I_x=\oint_\Gamma\left(y\,\mathrm{d}z-z\,\mathrm{d}y\right)$ $I_y=\oint_\Gamma\left(z\,\mathrm{d}x-x\,\mathrm{d}z\right)$ $I_z=\oint_\Gamma\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)$

Si nos fijamos, por ejemplo, en la tercera componente

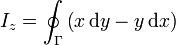
$I_z=\oint_\Gamma\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)$

vemos que el integrando es exactamente el mismo que en el caso de una curva plana. La curva de integración en este caso es tridimensional, pero, puesto que en el integrando aparecen solamente $x$ e $y$ , realmente los valores de $z$ son irrelevantes. Otra curva, con diferentes valores de $z$ , en particular, una curva que tuviera $z = 0$ , pero los mismos valores de $x$ e $y$ , daría el mismo resultado. Esto es, que esta componente es igual a la integral sobre la proyección de la curva $Γ$ en el plano $X Y$ . La proyección es una curva plana, y por tanto, para ella es aplicable el resultado del apartado anterior. Por tanto

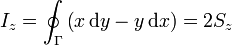
$I_z=\oint_\Gamma\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)=2S_z$

siendo $S z$ el área de la proyección de $Γ$ sobre el plano $z = 0$

De la misma manera se interpretan las otras dos componentes

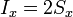
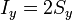
$I_x = 2S_x\,$ $I_y=2S_y\,$

o, reuniendo los tres resultados

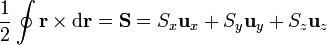
$\frac{1}{2}\oint\mathbf{r}\times\mathrm{d}\mathbf{r} = \mathbf{S}=S_x\mathbf{u}_x+S_y\mathbf{u}_y+S_z\mathbf{u}_z$

Siendo el vector superficie uno que tiene por componentes las áreas de las proyecciones de la curva $Γ$ sobre los tres planos coordenados.

En cuanto al signo de estas componentes, viene dado por la regla de la mano derecha. Si recorremos la proyección en $z = 0$ de tal forma que el vector normal (según esta regla) vaya en el mismo sentido que $\mathbf{u}_z$ , entonces el signo es positivo. En caso contrario es negativo.

2.3 Ejemplos

2.3.1 Curva plana en el espacio

UN caso particular de curva tridimensional es aquella que sí puede ser contenida en un plano, aunque éste no coincida con ninguno de los planos coordenados.

Los puntos de esta curva verifican la ecuación vectorial del plano

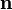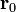No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathbf{n}\cdot(\mathbf{r}-\mathbf{r}_0\right) = 0

siendo $\mathbf{n}$ el vector unitario normal al plano y $\mathbf{r}_0$ un punto dado de éste. Podemos escribir entonces la curva como

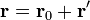
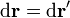
$\mathbf{r}=\mathbf{r}_0+\mathbf{r}'$ $\mathrm{d}\mathbf{r} = \mathrm{d}\mathbf{r}'$

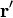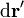donde tanto $\mathbf{r}'$ como $\mathrm{d}\mathbf{r}'$ son vectores ortogonales a $\mathbf{n}$

2.3.2 Una curva alabeada

@@ Línea 98: / Línea 98: @@
 ====Curva plana en el espacio====
 UN caso particular de curva tridimensional es aquella que sí puede ser contenida en un plano, aunque éste no coincida con ninguno de los planos coordenados.
+Los puntos de esta curva verifican la ecuación vectorial del plano
+<center><math>\mathbf{n}\cdot(\mathbf{r}-\mathbf{r}_0\right) = 0</math></center>
+siendo <math>\mathbf{n}</math> el vector unitario normal al plano y <math>\mathbf{r}_0</math> un punto dado de éste. Podemos escribir entonces la curva como
+<center><math>\mathbf{r}=\mathbf{r}_0+\mathbf{r}'</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{r} = \mathrm{d}\mathbf{r}'</math></center>
+donde tanto <math>\mathbf{r}'</math> como <math>\mathrm{d}\mathbf{r}'</math> son vectores ortogonales a <math>\mathbf{n}</math>
 ====Una curva alabeada====
 [[Categoría:Problemas de fundamentos matemáticos]]

Vector superficie

De Laplace

Revisión de 13:43 25 dic 2008

Contenido

1 Enunciado

2 Solución

2.1 caso de una curva plana

2.1.1 Interpretación geométrica

2.2 Caso de una curva alabeada

2.3 Ejemplos

2.3.1 Curva plana en el espacio

2.3.2 Una curva alabeada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES