Conservación de magnitudes en movimiento curvo

De Laplace

(Diferencias entre revisiones)

última version al 20:19 24 ene 2015

Contenido

1 Enunciado
2 Fuerza
3 Impulso
4 Momento cinético
5 Energía cinética
6 Interpretación de los resultados

1 Enunciado

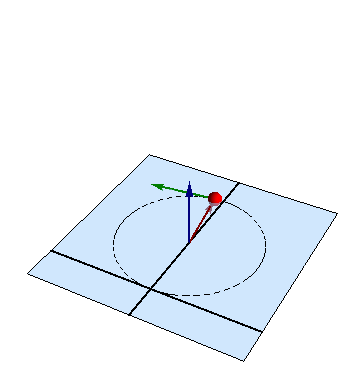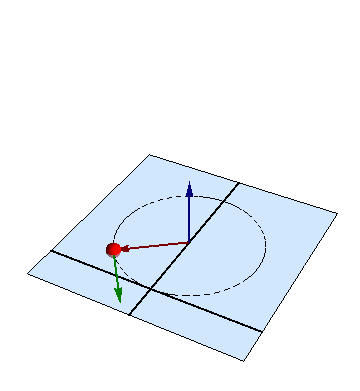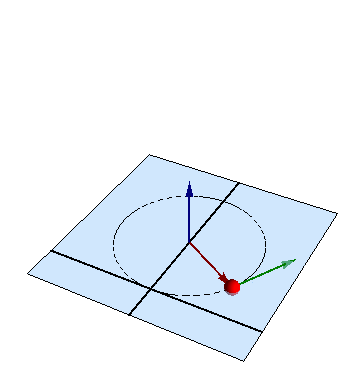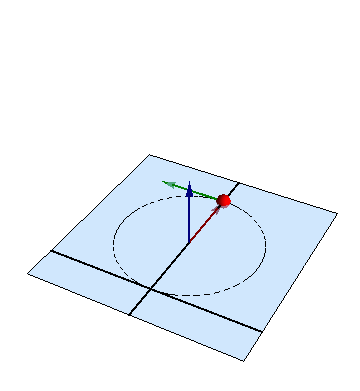
Una partícula de masa $m$ describe el movimiento plano

$\rho = A\,\mathrm{sen}(\Omega t)\qquad\varphi = \Omega t\qquad\qquad\ t \in(0,\pi/\Omega)$

Calcule la fuerza que actúa sobre la partícula en cualquier instante del intervalo.
Halle el impulso que experimenta entre $t = 0$ y $t = π / (2Ω)$ .
Demuestre que el momento cinético de la partícula respecto al origen no se conserva, pero respecto al punto 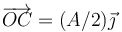$\overrightarrow{OC} = (A/2)\vec{\jmath}$ sí.
Calcule la energía cinética de la partícula. ¿Se conserva esta cantidad?

2 Fuerza

Podemos calcular la fuerza aplicando la segunda ley de Newton

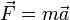
$\vec{F}=m\vec{a}$

Expresamos en primer lugar la posición en coordenadas cartesianas

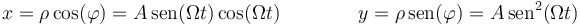
$x = \rho\cos(\varphi) = A\,\mathrm{sen}(\Omega t)\cos(\Omega t)\qquad \qquad y = \rho\,\mathrm{sen}(\varphi)=A\,\mathrm{sen}^2(\Omega t)$

Derivando una vez tenemos las componentes cartesianas de la velocidad

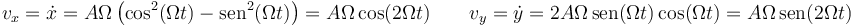
$v_x = \dot{x} = A\Omega\left(\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)\right) =A\Omega\cos(2\Omega t)\qquad v_y = \dot{y}=2A\Omega\,\mathrm{sen}(\Omega t)\cos(\Omega t)=A\Omega \,\mathrm{sen}(2\Omega t)$

y derivando una segunda vez las de la aceleración

$a_x=\ddot{x}=-2A\Omega^2\,\mathrm{sen}(\Omega t)\qquad\qquad a_y = \ddot{y}=2A\Omega^2 \cos(2\Omega t)$

lo que nos da la fuerza

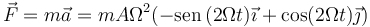
$\vec{F}=m\vec{a}=mA\Omega^2(-\mathrm{sen}\left(2\Omega t)\vec{\imath}+\cos(2\Omega t)\vec{\jmath}\right)$

3 Impulso

El impulso es igual al incremento de la cantidad de movimiento

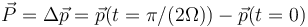
$\vec{P}=\Delta\vec{p}=\vec{p}(t=\pi/(2\Omega))-\vec{p}(t=0)$

Hallamos la cantidad de movimiento para todo instante, empleando las componentes de la velocidad que hallamos antes.

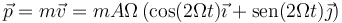
$\vec{p}=m \vec{v}=mA\Omega\left(\cos(2\Omega t)\vec{\imath}+\mathrm{sen}(2\Omega t)\vec{\jmath}\right)$

En los dos instantes indicados

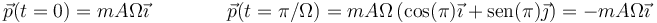
$\vec{p}(t=0)=mA\Omega \vec{\imath}\qquad\qquad \vec{p}(t=\pi/\Omega)= mA\Omega\left(\cos(\pi)\vec{\imath}+\mathrm{sen}(\pi)\vec{\jmath}\right)=-mA\Omega\vec{\imath}$

y por tanto

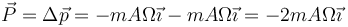
$\vec{P}=\Delta \vec{p}=-mA\Omega\vec{\imath}-mA\Omega\vec{\imath}= -2mA\Omega\vec{\imath}$

También podemos llegar a este resultado integrando la fuerza

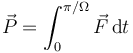
$\vec{P}=\int_0^{\pi/\Omega} \vec{F}\,\mathrm{d}t$

4 Momento cinético

La definición del momento cinético respecto al origen de coordenadas es

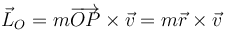
$\vec{L}_O = m\overrightarrow{OP}\times\vec{v}=m\vec{r}\times\vec{v}$

Para el caso de un movimiento plano esta cantidad se reduce a

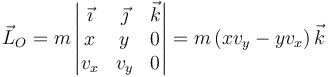
$\vec{L}_O = m\left|\begin{matrix} \vec{\imath}& \vec{\jmath} & \vec{k} \\ x & y & 0 \\ v_x & v_y & 0 \end{matrix}\right| = m\left(xv_y-yv_x\right)\vec{k}$

Sustituyendo las expresiones de las coordenadas y las componentes de la velocidad

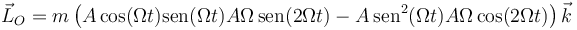
$\vec{L}_O = m\left(A\cos(\Omega t)\mathrm{sen}(\Omega t)A\Omega\,\mathrm{sen}(2\Omega t)-A\,\mathrm{sen}^2(\Omega t)A\Omega \cos(2\Omega t)\right)\vec{k}$

Sacando factor común

$\vec{L}_O = mA^2\Omega\,\mathrm{sen}(\Omega t)\left(\cos(\Omega t)\mathrm{sen}(2\Omega t)-\,\mathrm{sen}(\Omega t)\cos(2\Omega t)\right)\vec{k}=A^2\Omega\,\mathrm{sen}^2(\Omega t)\vec{k}$

Esta cantidad no es constante, sino que varía con el tiempo.

Consideremos ahora el momento cinético respecto al punto

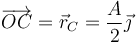
$\overrightarrow{OC}=\vec{r}_C=\frac{A}{2}\vec{\jmath}$

Para este punto tenemos

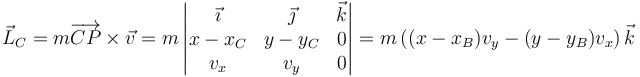
$\vec{L}_C=m\overrightarrow{CP}\times\vec{v}= m\left|\begin{matrix} \vec{\imath}& \vec{\jmath} & \vec{k} \\ x-x_C & y -y_C& 0 \\ v_x & v_y & 0 \end{matrix}\right| = m\left((x-x_B)v_y-(y-y_B)v_x\right)\vec{k}$

Sustituyendo las expresiones correspondientes

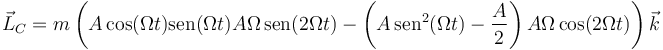
$\vec{L}_C = m\left(A\cos(\Omega t)\mathrm{sen}(\Omega t)A\Omega\,\mathrm{sen}(2\Omega t)-\left(A\,\mathrm{sen}^2(\Omega t)-\frac{A}{2}\right)A\Omega \cos(2\Omega t)\right)\vec{k}$

Operando aquí del mismo modo que antes

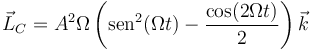
$\vec{L}_C = A^2\Omega\left(\mathrm{sen}^2(\Omega t)-\frac{\cos(2\Omega t)}{2}\right)\vec{k}$

Esto puede parecer que no es una constante. No obstante, aplicando relaciones trigonométricas

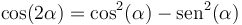
$\cos(2\alpha) = \cos^2(\alpha)-\mathrm{sen}^2(\alpha)\,$

queda

$\mathrm{sen}^2(\Omega t) -\frac{\cos(2\Omega t)}{2}=\mathrm{sen}^2(\Omega t)-\frac{\cos^2(\Omega t)-\mathrm{sen}^2(\Omega t)}{2}=-\frac{\cos^2(\Omega t)+\mathrm{sen}^2(\Omega t)}{2}=-\frac{1}{2}$

y por tanto

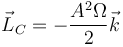
$\vec{L}_C = -\frac{A^2\Omega}{2}\vec{k}$

que efectivamente es un vector constante.

5 Energía cinética

Para hallar el valor de la energía cinética simplemente hallamos el cuadrado de la rapidez

$|\vec{v}|^2 = v_x^2+v_y^2 = A^2\Omega^2\cos^2(2\Omega t)+ A^2\Omega^2\mathrm{sen}^2(2\Omega t)=A^2\Omega^2$

El movimiento es uniforme y por tanto la energía cinética es una constante

$K = \frac{1}{2}m|\vec{v}|^2 = \frac{mA^2\Omega^2}{2}$

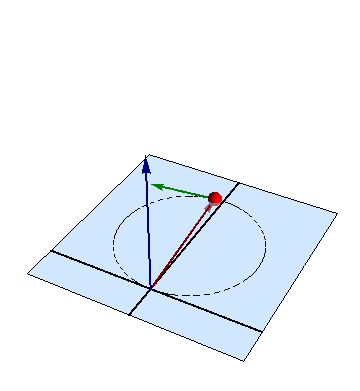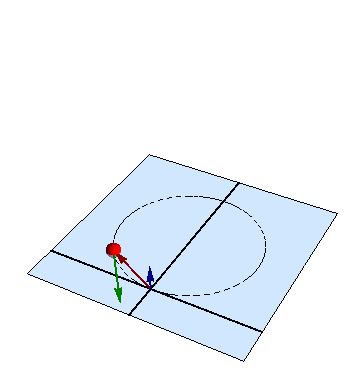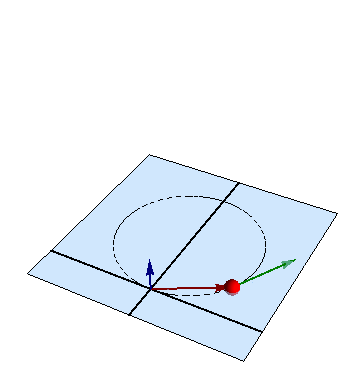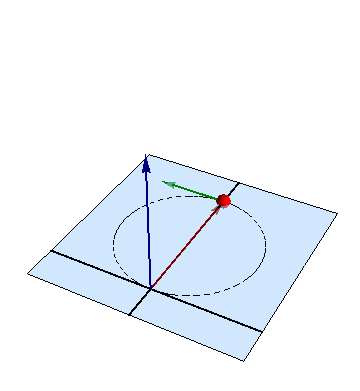
6 Interpretación de los resultados

Aunque las ecuaciones pueden no aparentarlo, el movimiento en este problema, como en otro similar, es uno circular uniforme, con velocidad angular

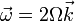
$\vec{\omega}=2\Omega\vec{k}$

en torno al centro

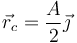
$\vec{r}_c = \frac{A}{2}\vec{\jmath}$

En un movimiento de esta clase:

La cantidad de movimiento no se conserva, ya que aunque el movimiento es uniforme (rapidez constante), la dirección de la velocidad va cambiando, por lo que no se conserva ésta, ni su producto por la masa. La cantidad de movimiento de una partícula solo se conserva en un movimiento rectilíneo y uniforme.
En un movimiento circular uniforme sí se conserva el momento cinético respecto al centro de la circunferencia, pero no respecto a ningún otro punto. El valor del momento cinético es, para este tipo de movimientos

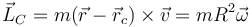
$\vec{L}_C = m(\vec{r}-\vec{r}_c)\times\vec{v}= mR^2\vec{\omega}$

En nuestro caso

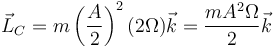
$\vec{L}_C = m\left(\frac{A}{2}\right)^2(2\Omega)\vec{k}= \frac{mA^2\Omega}{2}\vec{k}$

Por tratarse de un movimiento uniforme, la rapidez es constante y por tanto la energía cinética también se conserva.

Archivo:momento-cinetico-circular-01.gif

Archivo:momento-cinetico-circular-02.gif

@@ Línea 96: / Línea 96: @@
 y por tanto
-<center><math>\vec{L}_B = -\frac{A^2\Omega}{2}\vec{k}</math></center>
+<center><math>\vec{L}_C = -\frac{A^2\Omega}{2}\vec{k}</math></center>
 que efectivamente es un vector constante.

Conservación de magnitudes en movimiento curvo

De Laplace

última version al 20:19 24 ene 2015

Contenido

1 Enunciado

2 Fuerza

3 Impulso

4 Momento cinético

5 Energía cinética

6 Interpretación de los resultados

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES