Propiedades de rotores descentrados

De Laplace

(Diferencias entre revisiones)

Revisión de 21:37 12 dic 2014

Contenido

1 Enunciado
2 Introducción
- 2.1 Caso de una sola partícula
3 Rotor equilibrado
4 Rotor descentrado
5 Rotor inclinado
6 Masas desiguales

1 Enunciado

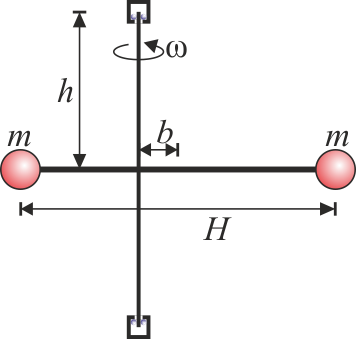
Se tiene un rotor formado por dos masas iguales de valor $m$ situadas en los extremos de una barra ideal (sin masa) de longitud $H$ . Cuando este rotor está equilibrado gira en torno a un eje perpendicular a la barra y que pasa por su centro. Este eje está anclado en dos rodamientos situados a una distancia $h$ del centro de la barra (uno por encima y otro por debajo de ella).

Calcule el momento cinético y la energía cinética (respecto a un sistema fijo y respecto al CM) si el rotor gira con velocidad angular constante $ω$ en torno al eje cuando:

Es horizontal y se encuentra centrado en el eje vertical.
Es horizontal pero se encuentra descentrado de forma que el eje no pasa por el centro de la barra, sino a una distancia b de éste.
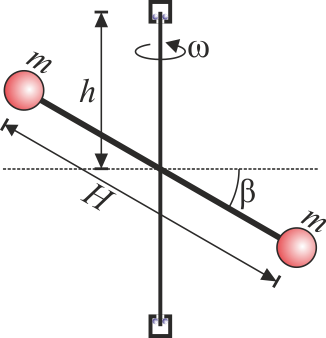
Está centrado pero la barra está inclinada respecto a la horizontal un ángulo β.
Es horizontal y se encuentra centrado en el eje vertical, pero las masas no son exactamente iguales, sino que valen $m 1$ y $m 2$ .

2 Introducción

Esta es la primera parte d eun problema de dinámica que continúa en otro problema. Se trata de analizar el comportamiento de un rotor formado por dos masas.

Aunque los casos son diferentes, especialmente en el aspecto dinámico de las fuerzas que se hallan en la segunda parte de este problema, el cálculo es similar en los cuatro casos, por lo que podemos hacer la mayor parte de los cálculos de forma general.

En todos los casos, tenemos dos masas $m 1$ y $m 2$ describiendo órbitas circulares en torno al eje.

$\vec{v}_1=\vec{\omega}\times\vec{r}_1 \qquad\qquad \vec{v}_2=\vec{\omega}\times\vec{r}_2$

El momento cinético del sistema será la suma de los de las dos partículas

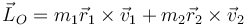
$\vec{L}_O = m_1\vec{r}_1\times\vec{v}_1 + m_2\vec{r}_2\times\vec{v}_2$

y de manera análoga para la energía cinética

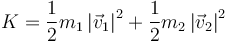
$K = \frac{1}{2}m_1\left|\vec{v}_1\right|^2+\frac{1}{2}m_2\left|\vec{v}_2\right|^2$

Para hallar los valores respecto al CM podemos aplicar las descomposiciones

$\vec{L}_O = M\vec{r}_C\times\vec{v}_C + \vec{L}_C\qquad\qquad K = \frac{1}{2}M\left|\vec{v}\right|^2 + K'$

2.1 Caso de una sola partícula

3 Rotor equilibrado

En el primer caso, las dos masas son iguales

$m_1=m_2=m\,\qquad\qquad M = m_1+m_2=2m$

las posiciones son simétricas respecto al eje

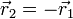
$\vec{r}_2=-\vec{r}_1$

y derivando, resultan también velocidades opuestas

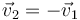
$\vec{v}_2=-\vec{v}_1$

Esto implica para el momento cinético que los dos sumandos son iguales

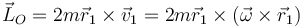
$\vec{L}_O = 2m\vec{r}_1\times\vec{v}_1 = 2m\vec{r}_1\times(\vec{\omega}\times\vec{r}_1)$

Desarrollamos el doble producto vectorial

$\vec{L}_O = 2m|\vec{r}_1|^2\vec{\omega}-2m(\vec{r}_1\cdot\vec{\omega})\vec{r}_1$

Puesto que el vector de posición es ortogonal a la velocidad angular, esto se reduce a

$\vec{L}_O = 2m\left(\frac{H}{2}\right)^2\vec{\omega}=\frac{MH^2}{4}\omega\vec{k}$

En este caso el momento cinético es proporcional a la velocidad angular, siendo la constante de proporcionalidad el llamado momento de inercia.

Puesto que el centro de masas coincide con el centro de la varilla también se cumple

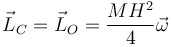
$\vec{L}_C=\vec{L}_O = \frac{MH^2}{4}\vec{\omega}$

Para la energía cinética el cálculo es similar. También son iguales las energías de las dos partículas.

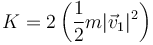
$K = 2\left(\frac{1}{2}m|\vec{v}_1|^2\right)$

Por tratarse de un movimiento circular uniforme la rapidez es igual a la velocidad angular multiplicada por el radio de giro

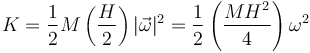
$K = \frac{1}{2}M\left(\frac{H}{2}\right)|\vec{\omega}|^2 = \frac{1}{2}\left(\frac{MH^2}{4}\right)\omega^2$

y, por coincidir el origen con el CM

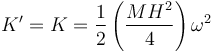
$K' = K = \frac{1}{2}\left(\frac{MH^2}{4}\right)\omega^2$

4 Rotor descentrado

En el segundo caso, las dos masas son de nuevo iguales

$m_1=m_2=m\,\qquad\qquad M = m_1+m_2=2m$

Las dos partículas describen de nuevo circunferencias horizontales, pero de distinto radio:

$R_1 = \frac{H}{2}+b\qquad\qquad R_2 = \frac{H}{2}-b$

Esto provoca que los dos sumandos en el momento cinético ya no sean iguales, pero cada uno se calcula como antes, empleando el radio correspondiente

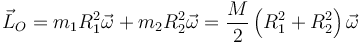
$\vec{L}_O = m_1R_1^2\vec{\omega}+m_2R_2^2\vec{\omega}=\frac{M}{2}\left(R_1^2+R_2^2\right)\vec{\omega}$

siendo

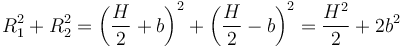
$R_1^2+R_2^2 =\left(\frac{H}{2}+b\right)^2+\left(\frac{H}{2}-b\right)^2=\frac{H^2}{2}+2b^2$

Nos queda finalmente

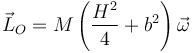
$\vec{L}_O=M\left(\frac{H^2}{4}+b^2\right)\vec{\omega}$

El centro de masas sigue estando en el centro de la varilla (que ya no coincide con el punto del eje). Este punto a una distancia $b$ del eje, describiendo una circunferencia con velocidad angular $\vec{\omega}$ . Por tanto el momento cinético por moverse con el CM valen

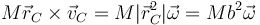
$M\vec{r}_C\times\vec{v}_C = M|\vec{r}_C^2|\vec{\omega}=Mb^2\vec{\omega}$

Restamos este término de la expresión completa y nos queda el momento cinético respecto al CM

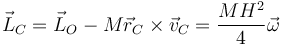
$\vec{L}_C = \vec{L}_O-M\vec{r}_C\times\vec{v}_C = \frac{MH^2}{4}\vec{\omega}$

Podemos ver que el momento respecto al CM es el mismo que en el caso simétrico.

5 Rotor inclinado

6 Masas desiguales

@@ Línea 16: / Línea 16: @@
 Aunque los casos son diferentes, especialmente en el aspecto dinámico de las fuerzas que se hallan en la segunda parte de este problema, el cálculo es similar en los cuatro casos, por lo que podemos hacer la mayor parte de los cálculos de forma general.
-En todos los casos, tenemos dos masas m_1 y m_2 describiendo órbitas circulares en torno al eje.
+En todos los casos, tenemos dos masas <math>m_1</math> y <math>m_2</math> describiendo órbitas circulares en torno al eje.
 <center><math>\vec{v}_1=\vec{\omega}\times\vec{r}_1 \qquad\qquad \vec{v}_2=\vec{\omega}\times\vec{r}_2</math></center>
@@ Línea 32: / Línea 32: @@
 <center><math>\vec{L}_O = M\vec{r}_C\times\vec{v}_C + \vec{L}_C\qquad\qquad K = \frac{1}{2}M\left|\vec{v}\right|^2 + K'</math></center>
+===Caso de una sola partícula===
 ==Rotor equilibrado==
 En el primer caso, las dos masas son iguales
-<center><math>m_1=m_2=m\,</math></center>
+<center><math>m_1=m_2=m\,\qquad\qquad M = m_1+m_2=2m</math></center>
 las posiciones son simétricas respecto al eje
@@ Línea 55: / Línea 56: @@
 Puesto que el vector de posición es ortogonal a la velocidad angular, esto se reduce a
-<center><math>\vec{L}_O = 2m\left(\frac{H}{2}\right)^2\vec{\omega}=\frac{MH^2}{4}\omega\vec{k} \qquad\qquad M = 2m</math></center>
+<center><math>\vec{L}_O = 2m\left(\frac{H}{2}\right)^2\vec{\omega}=\frac{MH^2}{4}\omega\vec{k}</math></center>
 En este caso el momento cinético es proporcional a la velocidad angular, siendo la constante de proporcionalidad el llamado momento de inercia.
@@ Línea 75: / Línea 76: @@
 <center><math>K' = K = \frac{1}{2}\left(\frac{MH^2}{4}\right)\omega^2</math></center>
+==Rotor descentrado==
+En el segundo caso, las dos masas son de nuevo iguales
+<center><math>m_1=m_2=m\,\qquad\qquad M = m_1+m_2=2m</math></center>
+Las dos partículas describen de nuevo circunferencias horizontales, pero de distinto radio:
+<center><math>R_1 = \frac{H}{2}+b\qquad\qquad R_2 = \frac{H}{2}-b</math></center>
+Esto provoca que los dos sumandos en el momento cinético ya no sean iguales, pero cada uno se calcula como antes, empleando el radio correspondiente
+<center><math>\vec{L}_O = m_1R_1^2\vec{\omega}+m_2R_2^2\vec{\omega}=\frac{M}{2}\left(R_1^2+R_2^2\right)\vec{\omega}</math></center>
+siendo
+<center><math>R_1^2+R_2^2 =\left(\frac{H}{2}+b\right)^2+\left(\frac{H}{2}-b\right)^2=\frac{H^2}{2}+2b^2</math></center>
+Nos queda finalmente
+<center><math>\vec{L}_O=M\left(\frac{H^2}{4}+b^2\right)\vec{\omega}</math></center>
+El centro de masas sigue estando en el centro de la varilla (que ya no coincide con el punto del eje). Este punto a una distancia <math>b</math> del eje, describiendo una circunferencia con velocidad angular <math>\vec{\omega}</math>. Por tanto el momento cinético por moverse con el CM valen
+<center><math>M\vec{r}_C\times\vec{v}_C = M|\vec{r}_C^2|\vec{\omega}=Mb^2\vec{\omega}</math></center>
+Restamos este término de la expresión completa y nos queda el momento cinético respecto al CM
+<center><math>\vec{L}_C = \vec{L}_O-M\vec{r}_C\times\vec{v}_C = \frac{MH^2}{4}\vec{\omega}</math></center>
+Podemos ver que el momento respecto al CM es el mismo que en el caso simétrico.
-==Rotor descentrado==
 ==Rotor inclinado==
 ==Masas desiguales==
 [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]]

Propiedades de rotores descentrados

De Laplace

Revisión de 21:37 12 dic 2014

Contenido

1 Enunciado

2 Introducción

2.1 Caso de una sola partícula

3 Rotor equilibrado

4 Rotor descentrado

5 Rotor inclinado

6 Masas desiguales

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES