Magnitudes en una máquina de Atwood
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Considere una máquina de Atwood ideal formada por dos masas <math>m_1</math> y <math>m_2</math> que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio …') |
|||
| Línea 6: | Línea 6: | ||
<center>[[Archivo:Esquema-maquina-atwood.png]]</center> | <center>[[Archivo:Esquema-maquina-atwood.png]]</center> | ||
| + | ==Propiedades del sistema== | ||
| + | ===Masa=== | ||
| + | ===Propiedades del CM=== | ||
| + | ====Posición==== | ||
| + | ====Velocidad==== | ||
| + | ====Aceleración==== | ||
| + | ===Cantidad de movimiento=== | ||
| + | ===Momento cinético=== | ||
| + | ===Energía cinética=== | ||
| + | ==Leyes de evolución== | ||
| + | ===Cantidad de movimiento=== | ||
| + | ===Momento cinético=== | ||
| + | ===Energía cinética=== | ||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
Revisión de 16:39 8 dic 2014
Contenido |
1 Enunciado
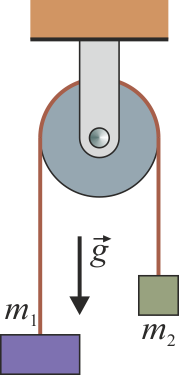
Considere una máquina de Atwood ideal formada por dos masas m1 y m2 que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio b a través de un hilo también ideal (inextensible y sin masa) de longitud l). Inicialmente las dos masas están en reposo a la misma altura.
- Determine la masa total, la posición, velocidad y aceleración del centro de masas, la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética del sistema, todo ello como función del tiempo.
- Para la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética determine sus derivadas respecto al tiempo y comprueba que se satisfacen las leyes para su evolución.