|
|
| Línea 1: |
Línea 1: |
| | [[F1 GIA PPC 2014, Partícula moviéndose sobre una parábola | Partícula moviéndose sobre una parábola]] | | [[F1 GIA PPC 2014, Partícula moviéndose sobre una parábola | Partícula moviéndose sobre una parábola]] |
| | [[Imagen:F1_GIA_PPC_2014_parabola.png|right]] | | [[Imagen:F1_GIA_PPC_2014_parabola.png|right]] |
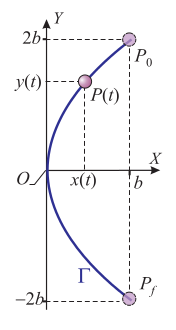
| - | Una partícula <math>P</math> realiza un movimiento en el plano <math>OXY</math> , cuya trayectoria <math>\Gamma</math>, y ley horaria para la
| |
| - | coordenada <math>y = y(t)</math>, están descritas por las expresiones:
| |
| - | <center>
| |
| - | <math>
| |
| - | \Gamma: x = \dfrac{1}{4b}y^2; \qquad y(t) = 2b-v_0t
| |
| - | </math>
| |
| - | </center>
| |
| - | siendo <math>b</math> y <math>v 0</math> constantes de valor positivo conocido. El movimiento se inicia en el instante <math>t=0</math>, cuando la partícula ocupa la posición de coordenadas <math>P_0(b,2b)</math>, y termina en la posición <math>P_f(b,-2b)</math>.
| |
| - |
| |
| - | # Indique cual de las siguientes expresiones paramétricas de <math>\overrightarrow{OP}=\vec{r}(\lambda)</math> describe correctamente la trayectoria <math>\Gamma</math> de la partícula
| |
| - | ##<math>\Gamma: \vec{r}(\lambda) = \lambda\,\vec{\imath} + 2\sqrt{b}\,\vec{\jmath};\quad 0\leq\lambda\leq b</math>
| |
| - | ##<math>\Gamma: \vec{r}(\lambda) = \dfrac{\lambda^2}{4b}\,\vec{\imath} - \lambda\,\vec{\jmath};\quad -2b\leq\lambda\leq 2b</math>
| |
| - | ##<math>\Gamma: \vec{r}(\lambda) = b[1-\cos(2\lambda)]\,\vec{\imath} +2b\mathrm{sen}\,(\lambda)\,\vec{\jmath};\quad -\pi/2\leq\lambda\leq \pi/2</math>
| |
| - | ##<math>\Gamma: \vec{r}(\lambda) = \dfrac{\lambda^2}{4b}\,\vec{\imath} + (2b-\lambda)\,\vec{\jmath};\quad 0\leq\lambda\leq 4b</math>
| |
| - | # Calcule el vector tangente a la trayectoria en un punto de coordenadas <math>P(x,y)</math>
| |
| - | #Sea <math>s(t)</math> la distancia medida a lo largo de la trayectoria, desde <math>P_0</math> hasta el punto en que se encuentra la partícula en el instante <math>t</math>. Indique cuál de las siguientes expresiones es la distancia que por unidad de tiempo recorre la partícula en dicho instante,
| |
| - | <center>
| |
| - | <math>
| |
| - | \dot{s}(t) = \dfrac{\mathrm{d}s(t)}{\mathrm{d}t} =
| |
| - | \left|\dfrac{\mathrm{d}\vec{r}(t)}{\mathrm{d}t}\right|
| |
| - | </math>
| |
| - | </center>
| |
| - | #¿En qué puntos de la trayectoria se anula la componente tangencial y/o la componente normal de la aceleración?
| |