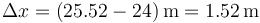Tiro parabólico con desnivel
De Laplace
(→Solución con barrera) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
En una partida de los [http://www.angrybirds.com/ Angry Birds] se debe lanzar un pájaro para alcanzar a un cerdo, siendo el movimiento del pájaro debido únicamente a la acción de la gravedad (se desprecia el rozamiento con el aire). | En una partida de los [http://www.angrybirds.com/ Angry Birds] se debe lanzar un pájaro para alcanzar a un cerdo, siendo el movimiento del pájaro debido únicamente a la acción de la gravedad (se desprecia el rozamiento con el aire). | ||
| - | El tirachinas con el que se lanza el pájaro se encuentra a una altura de | + | El tirachinas con el que se lanza el pájaro se encuentra a una altura de 7 m respecto al suelo en el que se halla el cerdo. Éste se encuentra a una distancia sobre la horizontal horizontal de 24 m del lanzador. |
| - | + | ||
| - | + | ||
Suponiendo que tanto el pájaro como el cerdo son objetos puntuales y que la barrera es de pequeño espesor, pero absolutamente rígida, calcule la rapidez y el ángulo de elevación respecto a la horizontal con los que debe lanzarse el pájaro, si la rapidez debe ser mínima. ¿Qué rapidez tiene el pájaro en el momento en que impacta con el cerdo? ¿Cuánto tarda en hacerlo? Tómese <math>g=9.81\,\mathrm{m}/\mathrm{s}^2</math>. | Suponiendo que tanto el pájaro como el cerdo son objetos puntuales y que la barrera es de pequeño espesor, pero absolutamente rígida, calcule la rapidez y el ángulo de elevación respecto a la horizontal con los que debe lanzarse el pájaro, si la rapidez debe ser mínima. ¿Qué rapidez tiene el pájaro en el momento en que impacta con el cerdo? ¿Cuánto tarda en hacerlo? Tómese <math>g=9.81\,\mathrm{m}/\mathrm{s}^2</math>. | ||
| Línea 12: | Línea 10: | ||
<center>[[Archivo:problema-angry.png]]</center> | <center>[[Archivo:problema-angry.png]]</center> | ||
==Introducción== | ==Introducción== | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Supongamos, para hacerlo general, que el pájaro se encuentra a una altura <math>z=h</math>, y el cerdo a una distancia horizontal <math>x=b</math> del punto de lanzamiento. | Supongamos, para hacerlo general, que el pájaro se encuentra a una altura <math>z=h</math>, y el cerdo a una distancia horizontal <math>x=b</math> del punto de lanzamiento. | ||
| Línea 82: | Línea 74: | ||
<center><math>\alpha=\frac{1}{2}\mathrm{arctg}\left(\frac{b}{h}\right)</math></center> | <center><math>\alpha=\frac{1}{2}\mathrm{arctg}\left(\frac{b}{h}\right)</math></center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
con | con | ||
| Línea 105: | Línea 93: | ||
que son las relaciones para el tiro parabólico horizontal. | que son las relaciones para el tiro parabólico horizontal. | ||
| - | En nuestro caso | + | En nuestro caso |
| - | <center><math>\alpha=\frac{1}{2}\mathrm{arctg}\left(\frac{ | + | <center><math>\alpha = \frac{1}{2}\mathrm{arctg}\left(\frac{24}{7}\right)</math></center> |
| - | + | En este caso, aplicando la relación trigonométrica | |
| - | <center><math> | + | <center><math>\mathrm{tg}(2\alpha)=\frac{2\,\mathrm{tg}(\alpha)}{1-\mathrm{tg}^2(\alpha)}</math></center> |
| - | + | puede obtenerse una expresión más sencilla para el ángulo | |
| - | + | <center><math>\alpha = \mathrm{arctg}\left(\frac{3}{4}\right)</math></center> | |
| - | + | es decir, | |
| - | + | <center><math>\mathrm{tg}(\alpha)=\frac{3}{4}\qquad\qquad\mathrm{sen}(\alpha)=\frac{3}{5}\qquad\qquad \cos(\alpha) = \frac{4}{5}</math></center> | |
| + | Para este ángulo, el cuadrado de la rapidez inicial cumple | ||
| + | |||
| + | <center><math>v_{0\mathrm{min}}^2 = \frac{gb^2}{2(h+b\,\mathrm{tg}(\alpha))\cos^2(\alpha)}</math></center> | ||
| + | |||
| + | que, numéricamente (tomando g = 9.81m/²) vale | ||
| + | |||
| + | <center><math>v_{0\mathrm{min}}^2 = 176.58\,\frac{\mathrm{m}}{\mathrm{s}^2}\qquad\Rightarrow\qquad v_{0\mathrm{min}}=13.3\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | La velocidad en cualquier instante es igual a | ||
| + | |||
| + | <center><math>\vec{v}(t)=v_0\cos(\alpha)\vec{\imath}+(v_0\,\mathrm{sen}(\alpha)-g t)\vec{k}</math></center> | ||
| + | |||
| + | Sustituyendo aquí el tiempo en función de la coordenada <math>x</math> | ||
| + | |||
| + | <center><math>\vec{v}(x)=v_0\cos(\alpha)\vec{\imath}+\left(v_0\,\mathrm{sen}(\alpha)-\frac{gx}{v_0\cos(\alpha)})\vec{k}\right)</math></center> | ||
| + | |||
| + | En el punto del impacto, hacemos <math>x=b</math>. Para el valor mínimo de la rapidez de lanzamiento, se puede simplificar a | ||
| + | |||
| + | <center><math>\vec{v}_i=v0\left(\cos(\alpha)\vec{\imath}-\frac{\cos^2(\alpha)}{\mathrm{sen}(\alpha)}\vec{k}\right)</math></center> | ||
| + | |||
| + | siendo la rapidez de impacto | ||
| + | |||
| + | <center><math>\left|\vec{v}_i\right| = v_0\mathrm{cotg}(\alpha)</math></center> | ||
| + | |||
| + | En nuestro caso | ||
| + | |||
| + | <center><math>\left|\vec{v}_i\right| = \frac{4}{3}v_0=17.72\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <!-- | ||
==Solución con barrera== | ==Solución con barrera== | ||
hemos demostrado que si el pájaro siguiera la trayectoria de rapidez mínima hacia el cerdo chocaría con la barrera, aunque si la barrera hubiera estado más cerca habría pasado por encima. | hemos demostrado que si el pájaro siguiera la trayectoria de rapidez mínima hacia el cerdo chocaría con la barrera, aunque si la barrera hubiera estado más cerca habría pasado por encima. | ||
| Línea 168: | Línea 188: | ||
la rapidez de impacto la podemos hallar calculando la velocidad y hallando su módulo, o aplicando que en un movimiento con aceleración constante | la rapidez de impacto la podemos hallar calculando la velocidad y hallando su módulo, o aplicando que en un movimiento con aceleración constante | ||
| - | <center><math>|\vec{v}|=\sqrt{v_0^2+2gh}= | + | <center><math>|\vec{v}|=\sqrt{v_0^2+2gh}=11.72\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> |
| - | + | --> | |
==Exceso de velocidad== | ==Exceso de velocidad== | ||
| + | Si manteniendo el ángulo de lanzamiento se le comunica al pájaro una rapidez inicial mayor, describirá una parábola más abierta y caerá más allá del cerdo | ||
| + | |||
| + | <center>[[Archivo:dos.parabolas-angry-02.png]]</center> | ||
| + | |||
| + | la nueva posición de impacto la calculamos con la ecuación de la parábola | ||
| + | |||
| + | <center><math>0 = h + \mathrm{tg}(\alpha) x - \frac{gx^2}{2v_0^2\cos^2(\alpha)}</math></center> | ||
| + | |||
| + | siendo la nueva rapidez inicial | ||
| + | |||
| + | <center><math>v_0=1.05v_{0\mathrm{min}}=13.95\,\frac{\mathrm{m}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | Esto da una ecuacion de segundo grado en x, con soluciones | ||
| + | |||
| + | <center><math>x_1= -6.83\,\mathrm{m}\qquad\qquad x_2= 25.52\,\mathrm{m}</math></center> | ||
| + | |||
| + | La primera solución la descartamos por ser negativa y queda un incremento en la distancia de | ||
| + | |||
| + | <center><math>\Delta x = (25.52-24)\,\mathrm{m}=1.52\,\mathrm{m}</math></center> | ||
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
última version al 10:47 9 nov 2014
1 Enunciado
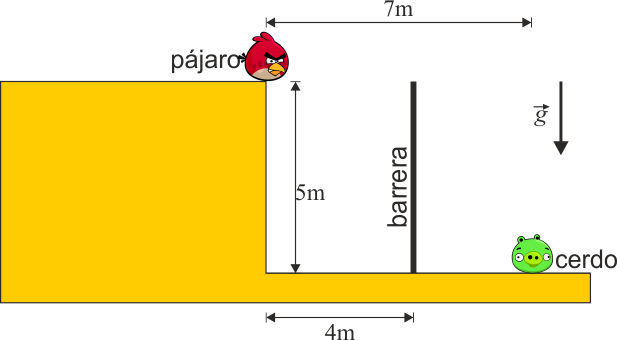
En una partida de los Angry Birds se debe lanzar un pájaro para alcanzar a un cerdo, siendo el movimiento del pájaro debido únicamente a la acción de la gravedad (se desprecia el rozamiento con el aire).
El tirachinas con el que se lanza el pájaro se encuentra a una altura de 7 m respecto al suelo en el que se halla el cerdo. Éste se encuentra a una distancia sobre la horizontal horizontal de 24 m del lanzador.
Suponiendo que tanto el pájaro como el cerdo son objetos puntuales y que la barrera es de pequeño espesor, pero absolutamente rígida, calcule la rapidez y el ángulo de elevación respecto a la horizontal con los que debe lanzarse el pájaro, si la rapidez debe ser mínima. ¿Qué rapidez tiene el pájaro en el momento en que impacta con el cerdo? ¿Cuánto tarda en hacerlo? Tómese 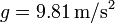 .
.
Suponga ahora que, por error, le comunicamos una rapidez mayor en un 5% a la que debería tener, pero manteniendo correcto el ángulo. ¿Cuánto más lejos o más cerca impacta el pájaro?
2 Introducción
Supongamos, para hacerlo general, que el pájaro se encuentra a una altura z = h, y el cerdo a una distancia horizontal x = b del punto de lanzamiento.
Una vez que el pájaro es lanzado describe un movimiento parabólico
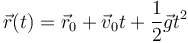
con las condiciones iniciales
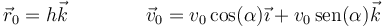
Separando en componentes nos quedan las ecuaciones horarias
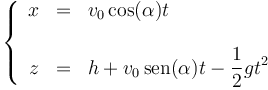
siendo v0 la rapidez inicial y α el ángulo de lanzamiento respecto a la horizontal.
Podemos eliminar el tiempo entre estas dos ecuaciones despejando en la primera y sustituyendo en la segunda. Queda la ecuación de la trayectoria parabólica
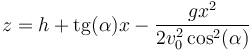
puesto que esta parábola debe pasar por el punto en que se halla el cerdo (x = b, z = 0), debe cumplirse

Tenemos infinitas parábolas que llevan del pájaro al cerdo, cada una con un ángulo de lanzamiento y una velocidad inicial correspondiente.
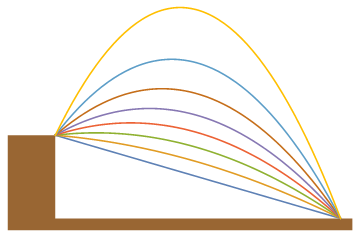
Podemos ver que hay un ángulo mínimo, que correspondería a que fuera en línea recta, tal que
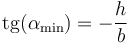
y uno máximo, que sería de 90°. Despejando de aquí, podemos obtener una relación entre la rapidez inicial y el ángulo de lanzamiento
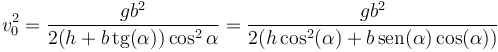
Podemos representar la rapidez inicial frente al ángulo de lanzamiento
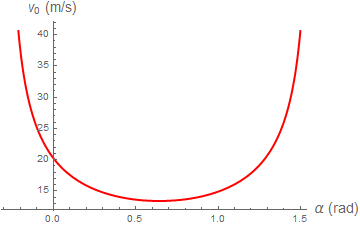
Esta gráfica muestra que la rapidez alcanza un valor mínimo.
Podemos ver por qué. Para conseguir que el pájaro vaya en línea recta hasta el cerdo, debe dispararse con tanta velocidad, que el efecto sea despreciable. Para alcanzarlo con un lanzamiento de casi 90° también debe comunicarse una gran rapidez, ya que si no caería casi al lado del punto de lanzamiento. Entre estos dos valores infinitos, habrá un valor mínimo.
Podemos hallar el ángulo para el cual rapidez es mínima derivando la expresión anterior

Aplicamos la regla para la derivada de un cociente
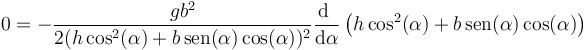
El cálculo se reduce a que se anule la última derivada, lo que da
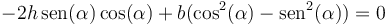
Podemos simplificar esta ecuación empleando las relaciones trigonométricas del ángulo doble

Finalmente, el ángulo de rapidez mínima es
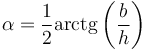
con
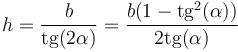
Sustituyendo esta relación en la ecuación anterior queda el resultado sencillo
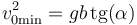
A modo de comprobación podemos ver qué ocurre si no hay desnivel, es decir si h = 0. Para este caso
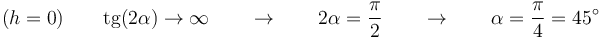
y
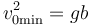
que son las relaciones para el tiro parabólico horizontal.
En nuestro caso
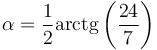
En este caso, aplicando la relación trigonométrica
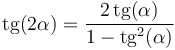
puede obtenerse una expresión más sencilla para el ángulo
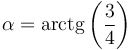
es decir,
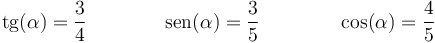
Para este ángulo, el cuadrado de la rapidez inicial cumple
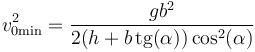
que, numéricamente (tomando g = 9.81m/²) vale

La velocidad en cualquier instante es igual a
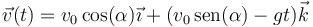
Sustituyendo aquí el tiempo en función de la coordenada x

En el punto del impacto, hacemos x = b. Para el valor mínimo de la rapidez de lanzamiento, se puede simplificar a

siendo la rapidez de impacto

En nuestro caso
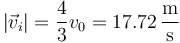
3 Exceso de velocidad
Si manteniendo el ángulo de lanzamiento se le comunica al pájaro una rapidez inicial mayor, describirá una parábola más abierta y caerá más allá del cerdo
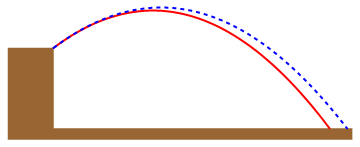
la nueva posición de impacto la calculamos con la ecuación de la parábola

siendo la nueva rapidez inicial
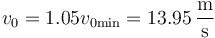
Esto da una ecuacion de segundo grado en x, con soluciones

La primera solución la descartamos por ser negativa y queda un incremento en la distancia de