1.4. Dependencias del periodo de un péndulo
De Laplace
(→Enunciado) |
(→Casos prácticos) |
||
| (13 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Un péndulo simple es una masa <math>m</math> suspendida de un hilo ideal (sin masa), que tiene una longitud <math>l</math>. La masa está sometida a la aceleración de la gravedad, <math>g</math>. El péndulo llega a separarse de la vertical un cierto ángulo <math>\theta_0</math>. | + | Un péndulo simple es una masa <math>m</math> suspendida de un hilo ideal (sin masa), que tiene una longitud <math>l</math>. La masa está sometida a la aceleración de la gravedad, <math>g</math>. El péndulo llega a separarse de la vertical un cierto ángulo máximo <math>\theta_0</math>. |
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre? | Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre? | ||
==Posibles dependencias== | ==Posibles dependencias== | ||
| - | El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, <math>l</math>; la aceleración de la gravedad, <math>g</math>; la masa <math>m</math>; y la amplitud inicial con la que se separa de la vertical,<math>\theta_0</math>. | + | El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, <math>l</math>; la aceleración de la gravedad, <math>g</math>; la masa, <math>m</math>; y la amplitud inicial con la que se separa de la vertical,<math>\theta_0</math>. |
| - | <center><math> | + | <center><math>\tau = f(m,l,g,\theta_0)\,</math></center> |
Sin embargo, esta función no es arbitraria, ya que la ecuación debe ser dimensionalmente correcta. Si el primer miembro tiene dimensiones de tiempo, el segundo debe tenerlo también. | Sin embargo, esta función no es arbitraria, ya que la ecuación debe ser dimensionalmente correcta. Si el primer miembro tiene dimensiones de tiempo, el segundo debe tenerlo también. | ||
| - | ¿Qué combinación de estos cuatro factores produce un tiempo? Tenemos que <math>m</math> tiene dimensiones de masa, <math>l</math> de longitud, <math>g</math> es una aceleración (LT | + | ¿Qué combinación de estos cuatro factores produce un tiempo? Tenemos que <math>m</math> tiene dimensiones de masa, <math>l</math> de longitud, <math>g</math> es una aceleración (<math>LT^{-2}</math>) y el ángulo inicial es adimensional. Para obtener un tiempo suponemos un producto de los diferentes factores elevados a ciertos exponentes n, p y q, que queremos determinar |
<center><math>m^n l^p g^q\,</math></center> | <center><math>m^n l^p g^q\,</math></center> | ||
| Línea 29: | Línea 29: | ||
y por tanto el periodo de oscilación del péndulo debe ser necesariamente de la forma | y por tanto el periodo de oscilación del péndulo debe ser necesariamente de la forma | ||
| - | <center><math> | + | <center><math>\tau = \sqrt{\frac{l}{g}}h(\theta_0)</math></center> |
| - | siendo <math> | + | siendo <math>h(\theta_0)</math> una cierta función de la amplitud de las oscilaciones. Esta función es desconocida por ahora, y para conocerla necesitamos resolver las ecuaciones de la dinámica del péndulo. |
No obstante, no precisamos el conocimiento de esta función para poder afirmar que el periodo de un péndulo simple no depende del valor la masa sujeta en su extremo (un péndulo ligero y uno pesado oscilarán en sincronía, para la misma amplitud inicial). | No obstante, no precisamos el conocimiento de esta función para poder afirmar que el periodo de un péndulo simple no depende del valor la masa sujeta en su extremo (un péndulo ligero y uno pesado oscilarán en sincronía, para la misma amplitud inicial). | ||
==Casos prácticos== | ==Casos prácticos== | ||
| - | A partir de la relación anterior podemos responder a preguntas concretas aunque desconozcamos la función <math> | + | A partir de la relación anterior podemos responder a preguntas concretas aunque desconozcamos la función <math>h(\theta_0)</math>. |
Si se duplica la longitud del hilo ¿cómo cambia el periodo? Suponemos que tenemos la misma amplitud en las oscilaciones. En ese caso | Si se duplica la longitud del hilo ¿cómo cambia el periodo? Suponemos que tenemos la misma amplitud en las oscilaciones. En ese caso | ||
| - | <center><math> | + | <center><math>\tau_1 = h(\theta_0)\sqrt{\frac{l_1}{g}}</math>{{qquad}}{{qquad}} |
| - | <math> | + | <math>\tau_2 = h(\theta_0)\sqrt{\frac{l_2}{g}}</math></center> |
Dividiendo la una por la otra | Dividiendo la una por la otra | ||
| - | <center><math>\frac{ | + | <center><math>\frac{\tau_2}{\tau_1} = \sqrt{\frac{l_2}{l_1}}</math></center> |
Si duplicamos la longitud | Si duplicamos la longitud | ||
| - | <center><math>\frac{ | + | <center><math>\frac{\tau_2}{\tau_1}=\sqrt{\frac{2l_1}{l_1}} = \sqrt{2}</math>{{tose}}<math> \tau_2 = 1.41\tau_1\,</math></center> |
El periodo, por tanto, aumenta en un 40%. | El periodo, por tanto, aumenta en un 40%. | ||
| Línea 55: | Línea 55: | ||
Si nos llevamos el péndulo a la Luna, ¿cómo varía el periodo? Operando igualmente | Si nos llevamos el péndulo a la Luna, ¿cómo varía el periodo? Operando igualmente | ||
| - | <center><math>\frac{ | + | <center><math>\frac{\tau_2}{\tau_1} = \sqrt{\frac{g_1}{g_2}} = \sqrt{\frac{g_1}{g_1/6}} = \sqrt{6}</math>{{tose}} <math>\tau_2 = 2.45\tau_1\,</math></center> |
El periodo es casi dos veces y media el que hay en la Tierra. Un reloj de péndulo situado en la Luna atrasará respecto a uno situado en la Tierra. | El periodo es casi dos veces y media el que hay en la Tierra. Un reloj de péndulo situado en la Luna atrasará respecto a uno situado en la Tierra. | ||
| - | [[Categoría:Problemas de metrología]] | + | [[Categoría:Problemas de metrología (G.I.T.I.)]] |
última version al 12:40 15 oct 2014
1 Enunciado
Un péndulo simple es una masa m suspendida de un hilo ideal (sin masa), que tiene una longitud l. La masa está sometida a la aceleración de la gravedad, g. El péndulo llega a separarse de la vertical un cierto ángulo máximo θ0.
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?
2 Posibles dependencias
El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, l; la aceleración de la gravedad, g; la masa, m; y la amplitud inicial con la que se separa de la vertical,θ0.
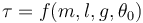
Sin embargo, esta función no es arbitraria, ya que la ecuación debe ser dimensionalmente correcta. Si el primer miembro tiene dimensiones de tiempo, el segundo debe tenerlo también.
¿Qué combinación de estos cuatro factores produce un tiempo? Tenemos que m tiene dimensiones de masa, l de longitud, g es una aceleración (LT − 2) y el ángulo inicial es adimensional. Para obtener un tiempo suponemos un producto de los diferentes factores elevados a ciertos exponentes n, p y q, que queremos determinar
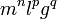
que tiene dimensiones
![\left[m^n l^p g^q\right]=M^n L^p (LT^{-2})^q = M^n L^{p+q} T^{-2q}](/wiki/images/math/2/9/8/298fbeb9e7d6d28682904209ead11f6e.png)
Puesto que esto debe ser igual a un tiempo (de dimensiones T1) los exponentes deben cumplir

de donde
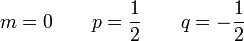
y por tanto el periodo de oscilación del péndulo debe ser necesariamente de la forma
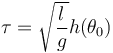
siendo h(θ0) una cierta función de la amplitud de las oscilaciones. Esta función es desconocida por ahora, y para conocerla necesitamos resolver las ecuaciones de la dinámica del péndulo.
No obstante, no precisamos el conocimiento de esta función para poder afirmar que el periodo de un péndulo simple no depende del valor la masa sujeta en su extremo (un péndulo ligero y uno pesado oscilarán en sincronía, para la misma amplitud inicial).
3 Casos prácticos
A partir de la relación anterior podemos responder a preguntas concretas aunque desconozcamos la función h(θ0).
Si se duplica la longitud del hilo ¿cómo cambia el periodo? Suponemos que tenemos la misma amplitud en las oscilaciones. En ese caso


Dividiendo la una por la otra

Si duplicamos la longitud
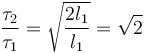


El periodo, por tanto, aumenta en un 40%.
Si nos llevamos el péndulo a la Luna, ¿cómo varía el periodo? Operando igualmente


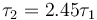
El periodo es casi dos veces y media el que hay en la Tierra. Un reloj de péndulo situado en la Luna atrasará respecto a uno situado en la Tierra.





