Primera Prueba de Control 2013/14 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(→Movimiento parabólico sobre un plano inclinado) |
(→Particula con un muelle horizontal y otro inclinado) |
||
| Línea 9: | Línea 9: | ||
==[[Particula con un muelle horizontal y otro inclinado, Noviembre 2013 (G.I.C.)| Particula con un muelle horizontal y otro inclinado]] == | ==[[Particula con un muelle horizontal y otro inclinado, Noviembre 2013 (G.I.C.)| Particula con un muelle horizontal y otro inclinado]] == | ||
| + | [[Imagen:Particula_muelle_horizontal_inclinado_GIC.png|right]] | ||
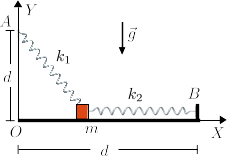
Un partícula de masa <math>m</math> reposa sobre un plano horizontal sin rozamiento. Está atada a dos muelles de constantes elásticas <math>k_1</math> y <math>k_2</math> y longitud natural nula, anclados en los puntos <math>A</math> y <math>B</math>. La partícula no puede desplazarse a lo largo del eje <math>OZ</math>. | Un partícula de masa <math>m</math> reposa sobre un plano horizontal sin rozamiento. Está atada a dos muelles de constantes elásticas <math>k_1</math> y <math>k_2</math> y longitud natural nula, anclados en los puntos <math>A</math> y <math>B</math>. La partícula no puede desplazarse a lo largo del eje <math>OZ</math>. | ||
última version al 13:05 1 oct 2014
1 Movimiento parabólico sobre un plano inclinado
Una partícula de masa m desliza sin rozamiento sobre un plano inclinado un ángulo α sobre la horizontal. La partícula parte desde el origen con una velocidad paralela a la base del plano y módulo v0, como se indica en la figura.
- Dibuja el diagrama de cuerpo libre de la partícula.
- Determina la velocidad de la partícula en cada instante.
- Determina la posición de la partícula en cada instante.
- Calcula el tiempo que tarda en llegar a la base del plano inclinado.
- ¿Qué tipo de curva describe la partícula?
2 Particula con un muelle horizontal y otro inclinado
Un partícula de masa m reposa sobre un plano horizontal sin rozamiento. Está atada a dos muelles de constantes elásticas k1 y k2 y longitud natural nula, anclados en los puntos A y B. La partícula no puede desplazarse a lo largo del eje OZ.
- Dibuja el diagrama de cuerpo libre de la partícula.
- Condición para que la masa no se separe del plano.
- Posición de equilibrio de la partícula en la situación del apartado anterior.
- Supongamos que existe rozamiento entre la partícula y el plano, con un coeficiente de rozamiento estático μe. Si xm es la coordenada de la partícula sobre el eje OX, en situación de equilibrio, calcula el módulo de la fuerza de rozamiento.