Entrar Página Discusión Historial Go to the site toolbox

Cuatro conductores paralelos

De Laplace

(Diferencias entre revisiones)
Línea 14: Línea 14:
¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?
¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?
==Potenciales y cargas iniciales==
==Potenciales y cargas iniciales==
 +
La forma más sencilla de resolver este problema es mediante un circuito equivalente.
 +
 +
Para construir este circuito sustituimos cada conductor por un nodo. Cada par de placas enfrentadas  forma un condensador plano, de capacidad
 +
 +
<center><math>C=\frac{\varepsilon S}{d}</math></center>
 +
 +
siendo
 +
 +
<center><math>S=L^2 =(0.2\,\mathrm{m})^2 = 0.04\,\mathrm{m}^2</math></center>
 +
 +
la sección de las placas y <math>d</math> la distancia entre placas, que es distinta en cada caso. Las capacidades de los tres condensadores son
 +
 +
;Entre el conductor 1 y el 2:
 +
<center><math>C_a=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.003\,\mathrm{m}}=400\,\mathrm{pF}</math></center>
 +
 +
;Entre el 2 y el 3:
 +
<center><math>C_b=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.002\,\mathrm{m}}=600\,\mathrm{pF}</math></center>
 +
 +
;Entre el 3 y el 4:
 +
<center><math>C_c=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.001\,\mathrm{m}}=1200\,\mathrm{pF}</math></center>
 +
 +
El circuito equivalente al sistema sería entonces el siguiente:
 +
 +
<center>[[Archivo:circuito-cuatro-bloques-01.png]]</center>
 +
 +
O, puesto de otra manera equivalente
 +
 +
<center>[[Archivo:circuito-cuatro-bloques-02.png]]</center>
 +
 +
Dado que el conductor 3 está descargado, los condensadores b y c están en serie, cumpliendo su capacidad equivalente
 +
 +
<center><math>\frac{1}{C_{bc}}=\frac{1}{C_b}+\frac{1}{C_c}=\frac{1}{600\,\mathrm{pF}}+\frac{1}{1200\,\mathrm{pF}}=\frac{1}{400\,\mathrm{pF}}\qquad\Rightarrow\qquad C_{bc}=400\,\mathrm{pF}</math></center>
 +
 +
Este condensador está en paralelo con el a, siendo la capacidad equivalente de la asociación completa
 +
 +
<center><math>C_{abc}=C_a+C_{bc}=800\,\mathrm{pF}</math></center>
 +
 +
Esto nos da la carga del conductor 2, que corresponde a la placa positiva de este conductor equivalente
 +
 +
<center><math>Q_2=C_{abc}(V_2-0) = 800\,\mathrm{pF}\times 125\,\mathrm{V}=100\,\mathrm{nC}</math></center>
 +
{| class="bordeado"
{| class="bordeado"
|-
|-

Revisión de 23:21 15 sep 2014

Contenido

1 Enunciado

Se tiene un sistema de conductores en forma de bloques prismáticos cuadrados de lado 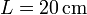L=20\,\mathrm{cm} de lado y grosor 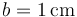b=1\,\mathrm{cm}. Estos bloques se sitúan paralelamente de forma que entre el primero y el segundo hay un espacio 3a; entre el 2º y el 3º hay 2a y entre el 3\tss{o} y el 4º hay a, siendo 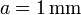a=1\,\mathrm{mm}. 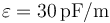El espacio entre los conductores está lleno de un dieléctrico ideal de permitividad \varepsilon=30\,\mathrm{pF}/\mathrm{m}.

El conductor 1 y el 4 se encuentran permanentemente a tierra.

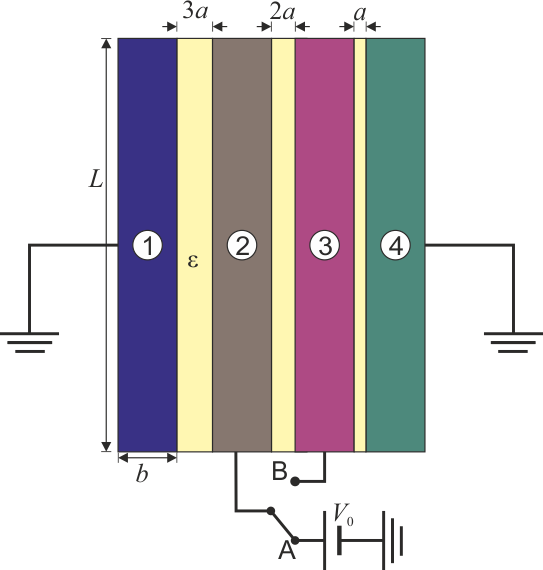
Archivo:fuente-cuatro-bloques.png

Inicialmente el interruptor se encuentra en la posición A, de forma que el conductor 2 se encuentra a un potencial 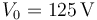V_0=125\,\mathrm{V}$, mientras que el 3 está aislado y descargado.

  1. Calcule el potencial del conductor 3, así como las cargas netas en cada uno de los cuatro conductores.
  2. Halle el campo eléctrico en cada uno de los espacios entre conductores, y las cargas almacenadas en cada una de las superficies conductoras
  3. Suponga que bruscamente se pasa el interruptor de la posición A a la B, conectando los conductores 2 y 3, ¿cómo quedan en ese caso las cargas y potenciales de los diferentes conductores, así como las cargas de cada una de las superficies?
  4. Halle la energía almacenada en el sistema antes y después de mover el interruptor.

¿Cuánta energía se disipa en el proceso?, ¿cómo puede haber desaparecido esta energía?

2 Potenciales y cargas iniciales

La forma más sencilla de resolver este problema es mediante un circuito equivalente.

Para construir este circuito sustituimos cada conductor por un nodo. Cada par de placas enfrentadas forma un condensador plano, de capacidad

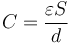
C=\frac{\varepsilon S}{d}

siendo

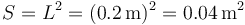
S=L^2 =(0.2\,\mathrm{m})^2 = 0.04\,\mathrm{m}^2

la sección de las placas y d la distancia entre placas, que es distinta en cada caso. Las capacidades de los tres condensadores son

Entre el conductor 1 y el 2
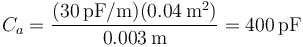
C_a=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.003\,\mathrm{m}}=400\,\mathrm{pF}
Entre el 2 y el 3
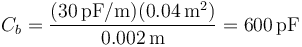
C_b=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.002\,\mathrm{m}}=600\,\mathrm{pF}
Entre el 3 y el 4
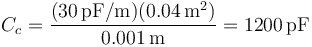
C_c=\frac{(30\,\mathrm{pF}/\mathrm{m})(0.04\,\mathrm{m}^2)}{0.001\,\mathrm{m}}=1200\,\mathrm{pF}

El circuito equivalente al sistema sería entonces el siguiente:

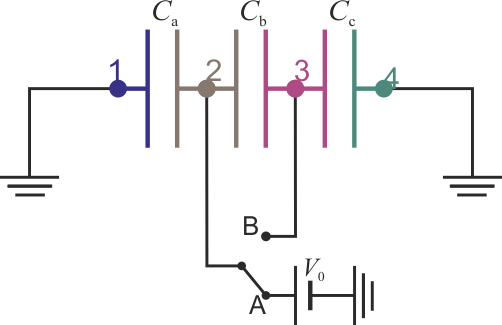
Archivo:circuito-cuatro-bloques-01.png

O, puesto de otra manera equivalente

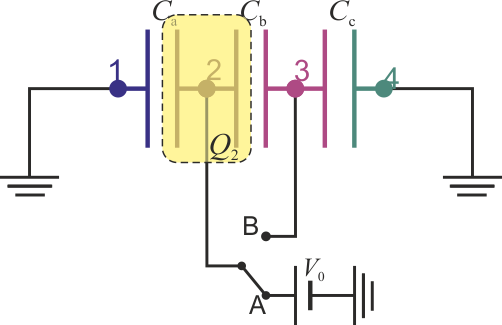
Archivo:circuito-cuatro-bloques-02.png

Dado que el conductor 3 está descargado, los condensadores b y c están en serie, cumpliendo su capacidad equivalente

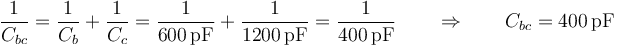
\frac{1}{C_{bc}}=\frac{1}{C_b}+\frac{1}{C_c}=\frac{1}{600\,\mathrm{pF}}+\frac{1}{1200\,\mathrm{pF}}=\frac{1}{400\,\mathrm{pF}}\qquad\Rightarrow\qquad C_{bc}=400\,\mathrm{pF}

Este condensador está en paralelo con el a, siendo la capacidad equivalente de la asociación completa

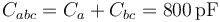
C_{abc}=C_a+C_{bc}=800\,\mathrm{pF}

Esto nos da la carga del conductor 2, que corresponde a la placa positiva de este conductor equivalente

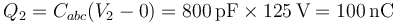
Q_2=C_{abc}(V_2-0) = 800\,\mathrm{pF}\times 125\,\mathrm{V}=100\,\mathrm{nC}
Conductor Q (nC) V (V)
1 -50 0
2 100 125
3 0 41.7
4 -50 0

3 Campo y cargas en cada superficie

4 Estado tras la conexión

Conductor Q (nC) V (V)
1 -75 0
2 75 62.5
3 25 62.5
4 -25 0

5 Balance energético

Antes de la conexión
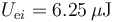
U_{\mathrm{e}i}=6.25\,\mu\mathrm{J}
Después de la conexión
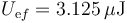
U_{\mathrm{e}f}=3.125\,\mu\mathrm{J}
Energía disipada
\Delta U = -3.125\,\mu\mathrm{J}
Obtenido de "http://tesla.us.es/wiki/index.php/Cuatro_conductores_paralelos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace