Rodadura y pivotamiento de una esfera
De Laplace
(Página creada con '==Enunciado== Una esfera maciza de 2.5 cm de radio y 0.400 kg de masa rueda y pivota sin deslizar sobre una superficie horizontal. En un instante dado la velocidad…') |
|||
| Línea 15: | Línea 15: | ||
==Velocidad angular y eje== | ==Velocidad angular y eje== | ||
| + | La velocidad angular de pivotamiento corresponde a un giro alrededor del eje OZ. Por ser en sentido antihorario, su sentido es el de <math>+\vec{k}</math> | ||
| + | |||
| + | <center><math>\vec{\omega}_p=\omega_p\vec{k}=1.80\,\vec{k}\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | La de rodadura es en la dirección y sentido que se nos indica | ||
| + | |||
| + | <center><math>\vec{\omega}_r=2.40\left(0.8\vec{\imath}+0.6\vec{\jmath}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}=\left(1.92\vec{\imath}+1.44\vec{\jmath}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
| + | |||
| + | La velocidad angular del sólido es la suma de las dos | ||
| + | |||
| + | \vec{\omega}=\vec{\omega}_p+\vec{\omega}_r=\left(1.92\vec{\imath}+1.44\vec{\jmath}+1.80\,\vec{k}\right)\,\frac{\mathrm{rad}}{\mathrm{s}} | ||
==Velocidad y rapidez del CM== | ==Velocidad y rapidez del CM== | ||
==Distancia al eje== | ==Distancia al eje== | ||
Revisión de 11:24 14 sep 2014
Contenido |
1 Enunciado
Una esfera maciza de 2.5 cm de radio y 0.400 kg de masa rueda y pivota sin deslizar sobre una superficie horizontal. En un instante dado la velocidad angular de pivotamiento es de 1.80 rad/s en sentido antihorario respecto al eje OZ (tomando como origen el punto de contacto y como eje OZ el perpendicular al plano), mientras que la de rodadura es de 2.40 rad/s en la dirección del vector unitario
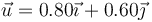
Para este instante, calcule:
- El vector velocidad angular y la ecuación del eje instantáneo de rotación.
- La velocidad y la rapidez del centro de la esfera.
- La distancia del centro de la esfera al eje instantáneo de rotación.
- La cantidad de movimiento, el momento cinético y la energía cinética de la esfera.
Dato: Momento de inercia de una esfera respecto a un eje que pasa por su centro I = (2 / 5)MR2.
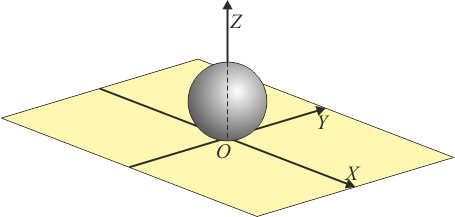
2 Velocidad angular y eje
La velocidad angular de pivotamiento corresponde a un giro alrededor del eje OZ. Por ser en sentido antihorario, su sentido es el de 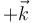
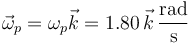
La de rodadura es en la dirección y sentido que se nos indica
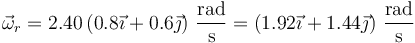
La velocidad angular del sólido es la suma de las dos
\vec{\omega}=\vec{\omega}_p+\vec{\omega}_r=\left(1.92\vec{\imath}+1.44\vec{\jmath}+1.80\,\vec{k}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}





