Dos esferas conductoras dentro de otra
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Se tiene un sistema de tres conductores esféricos. Uno de ellos (“2”) es una esfera de radio 54 mm con dos huecos esféricos, de radios 36&thin…') |
(→Enunciado) |
||
| Línea 9: | Línea 9: | ||
# ¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia? | # ¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia? | ||
# Halle la potencia instantánea disipada en el cable justo tras la conexión. | # Halle la potencia instantánea disipada en el cable justo tras la conexión. | ||
| + | |||
| + | <center>[[Archivo:tres-esferas-conductoras.png|300px]]</center> | ||
Tómese | Tómese | ||
<center><math>\frac{1}{4\pi\varepsilon_0}\simeq 9\times 10^9\,\frac{\mathrm{m}}{\mathrm{F}}</math></center> | <center><math>\frac{1}{4\pi\varepsilon_0}\simeq 9\times 10^9\,\frac{\mathrm{m}}{\mathrm{F}}</math></center> | ||
| - | |||
| - | [[Categoría:Problemas de electrostática en | + | |
| + | [[Categoría:Problemas de electrostática en medios materiales (GIE)]] | ||
Revisión de 12:49 26 jun 2014
Enunciado
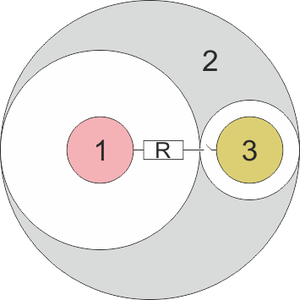
Se tiene un sistema de tres conductores esféricos. Uno de ellos (“2”) es una esfera de radio 54 mm con dos huecos esféricos, de radios 36 mm y 18 mm. En el centro de cada hueco se encuentran sendas esferas metálicas de radio 12 mm, siendo “1” la que está en el hueco grande y “3” la que está en el pequeño. Entre las esferas hay vacío y no hay más conductores ni cargas en el sistema.
Inicialmente la esfera “1” contiene una carga 120 nC mientras que los otros dos conductores están aislados y descargados.
- Halle el potencial de cada conductor, así como la energía almacenada en el sistema.
- Se conectan las dos esferas interiores mediante un hilo de resistencia 1 kΩ. Una vez que se ha vuelto a alcanzar el estado final, ¿cuáles son los nuevos potenciales de los conductores?
- ¿Cuál es la nueva energía almacenada? ¿Cuánta energía se ha disipado en la resistencia?
- Halle la potencia instantánea disipada en el cable justo tras la conexión.
Tómese