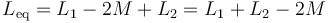Autoinducción e inducción mutua de bobinas
De Laplace
| (Una edición intermedia no se muestra.) | |||
| Línea 9: | Línea 9: | ||
==Matriz de inducciones mutuas== | ==Matriz de inducciones mutuas== | ||
| - | Existen tres métodos a la hora de calcular los coeficientes de inducción mutua y autoinducción. Uno es el cálculo directo a partir de la fórmula de Neumann, que no consideraremos por ser extremadamente complicado. El segundo es partir del flujo inducido en cada solenoide por los campos magnéticos propios o ajenos. El tercero es a partir de la expresión de la energía magnética | + | Existen tres métodos a la hora de calcular los coeficientes de inducción mutua y autoinducción. Uno es el cálculo directo a partir de la fórmula de Neumann, que no consideraremos por ser extremadamente complicado. El segundo es partir del flujo inducido en cada solenoide por los campos magnéticos propios o ajenos. El tercero es a partir de la expresión de la energía magnética, que tampoco consideraremos aquí (puede encontrarse en esta [[Inducción mutua de dos solenoides cilíndricos|versión extendida]] de este mismo problema |
| - | |||
| - | |||
| - | |||
[[Imagen:Campo1bobina.gif|right]] | [[Imagen:Campo1bobina.gif|right]] | ||
| Línea 45: | Línea 42: | ||
donde <math>I_1</math>, e <math>I_2</math> son las corrientes que circulan por los solenoides de radios <math>a</math> y <math>b</math>, respectivamente. Aquí hemos hecho uso de que todas las bobinas poseen la misma longitud y el mismo sentido de giro (lo que hace que todos los campos tengan el mismo sentido). | donde <math>I_1</math>, e <math>I_2</math> son las corrientes que circulan por los solenoides de radios <math>a</math> y <math>b</math>, respectivamente. Aquí hemos hecho uso de que todas las bobinas poseen la misma longitud y el mismo sentido de giro (lo que hace que todos los campos tengan el mismo sentido). | ||
| - | + | Para calcular los coeficientes de inducción mutua a partir de los flujos, partimos de las expresiones | |
| - | + | <center><math>\begin{matrix}\Phi_1 & = & L_{1}I_1+MI_2\\ \Phi_2 & = & MI_1+L_{2}I_2\end{matrix}</math></center> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | <center><math>\begin{matrix}\Phi_1 & = & L_{ | + | |
[[Imagen:FlujoL12.gif|left]] | [[Imagen:FlujoL12.gif|left]] | ||
| - | Si suponemos que <math>I_1=0</math>, <math>I_2\neq 0</math>, sólo circula corriente por la bobina exterior, resultan los coeficientes <math> | + | Si suponemos que <math>I_1=0</math>, <math>I_2\neq 0</math>, sólo circula corriente por la bobina exterior, resultan los coeficientes <math>M</math> y <math>L_{2}</math>. En este caso, el campo magnético vale |
| - | <center><math>\vec{B}=\begin{cases}\displaystyle \frac{\mu_0N_2I_2}{h}\ | + | <center><math>\vec{B}=\begin{cases}\displaystyle \frac{\mu_0N_2I_2}{h}\vec{k} & (\rho < b) \\ \mathbf{0} & (\rho > b)\end{cases}</math></center> |
[[Imagen:FlujoL22.gif|right]] | [[Imagen:FlujoL22.gif|right]] | ||
| Línea 85: | Línea 57: | ||
<center><math>\Phi_1=N_1(\pi a^2) \frac{\mu_0 N_2 I_2}{h}\quad \Rightarrow \quad | <center><math>\Phi_1=N_1(\pi a^2) \frac{\mu_0 N_2 I_2}{h}\quad \Rightarrow \quad | ||
| - | + | M=\frac{\mu_0\pi N_1N_2 a^2}{h}</math></center> | |
<center><math>\Phi_2=N_2(\pi b^2) \frac{\mu_0 N_2 I_2}{h}\quad \Rightarrow \quad | <center><math>\Phi_2=N_2(\pi b^2) \frac{\mu_0 N_2 I_2}{h}\quad \Rightarrow \quad | ||
| - | L_{ | + | L_{2}=\frac{\mu_0\pi N_2^2 b^2}{h}</math></center> |
| - | Aprovechando la simetría de los coeficientes, con el resultado anterior ya conocemos el coeficiente <math> | + | Aprovechando la simetría de los coeficientes, con el resultado anterior ya conocemos el coeficiente <math>M</math>, pero podemos hallarlos explícitamente empleando un razonamiento análogo. |
[[Imagen:FlujoL11.gif|left]][[Imagen:FlujoL21.gif|right]] | [[Imagen:FlujoL11.gif|left]][[Imagen:FlujoL21.gif|right]] | ||
| Línea 97: | Línea 69: | ||
<center><math>\Phi_1=N_1(\pi a^2) \frac{\mu_0 N_1 I_1}{h}\quad \Rightarrow \quad | <center><math>\Phi_1=N_1(\pi a^2) \frac{\mu_0 N_1 I_1}{h}\quad \Rightarrow \quad | ||
| - | L_{ | + | L_{1}=\frac{\mu_0\pi N_1^2 a^2}{h}</math></center> |
<center><math>\Phi_2=N_2(\pi a^2) \frac{\mu_0 N_1 I_1}{h}\quad \Rightarrow \quad | <center><math>\Phi_2=N_2(\pi a^2) \frac{\mu_0 N_1 I_1}{h}\quad \Rightarrow \quad | ||
| - | + | M=\frac{\mu_0\pi N_1N_2 a^2}{h}</math></center> | |
Finalmente, la matriz de inducciones mutuas es | Finalmente, la matriz de inducciones mutuas es | ||
| Línea 106: | Línea 78: | ||
<center><math>\mathsf{L}=\frac{\mu_0\pi}{h}\begin{pmatrix}N_1^2a^2 & N_1N_2a^2 \\ N_1N_2a^2 & N_2b^2\end{pmatrix}</math></center> | <center><math>\mathsf{L}=\frac{\mu_0\pi}{h}\begin{pmatrix}N_1^2a^2 & N_1N_2a^2 \\ N_1N_2a^2 & N_2b^2\end{pmatrix}</math></center> | ||
| - | Obsérvese como la simetría de la matriz resulta de aplicar razonamientos diferentes al elemento <math> | + | Obsérvese como la simetría de la matriz resulta de aplicar razonamientos diferentes al elemento <math>M</math> (en un caso es el área la que está limitada, en el otro es el campo magnético). |
==Constante de acoplamiento== | ==Constante de acoplamiento== | ||
La constante de acoplamiento para un sistema de dos solenoides vale | La constante de acoplamiento para un sistema de dos solenoides vale | ||
| - | <center><math>k = \frac{M}{\sqrt{L_1L_2}}=\frac{ | + | <center><math>k = \frac{M}{\sqrt{L_1L_2}}=\frac{M}{\sqrt{L_{1}L_{2}}}</math></center> |
Sustituyendo los valores para este caso | Sustituyendo los valores para este caso | ||
| Línea 117: | Línea 89: | ||
<center><math>k = \frac{N_1N_2a^2}{\sqrt{N_1^2a^2N_2^2b^2}} = \frac{a}{b}</math></center> | <center><math>k = \frac{N_1N_2a^2}{\sqrt{N_1^2a^2N_2^2b^2}} = \frac{a}{b}</math></center> | ||
| - | Esta es siempre menor que la unidad pues en el cálculo de <math> | + | Esta es siempre menor que la unidad pues en el cálculo de <math>M</math> hemos supuesto que <math>a \leq b</math>. Es igual a la unidad cuando <math>a=b\,</math>. En este caso, al tener las dos bobinas el mismo radio (aunque distinto número de espiras) todo el campo de una pasa por el interior de la otra y el acoplamiento es máximo |
==Asociación en serie== | ==Asociación en serie== | ||
| Línea 125: | Línea 97: | ||
*Calcular el flujo magnético en el sistema | *Calcular el flujo magnético en el sistema | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Si consideramos el sistema formado por las dos bobinas conectados por su extremo superior, el flujo magnético total a través de este sistema incluye los flujos a través de las N_1 espiras interiores y las N_2 exteriores. Pero teniendo en cuenta que la bobina exterior la recorremos en sentido contrario, la normal a las espiras exteriores va en sentido contrario a la normal de las interiores y por tanto | Si consideramos el sistema formado por las dos bobinas conectados por su extremo superior, el flujo magnético total a través de este sistema incluye los flujos a través de las N_1 espiras interiores y las N_2 exteriores. Pero teniendo en cuenta que la bobina exterior la recorremos en sentido contrario, la normal a las espiras exteriores va en sentido contrario a la normal de las interiores y por tanto | ||
| Línea 164: | Línea 107: | ||
de donde obtenemos de nuevo la autoinducción equivalente | de donde obtenemos de nuevo la autoinducción equivalente | ||
| - | <center><math>L_\mathrm{eq} = L_{ | + | <center><math>L_\mathrm{eq} = L_{1}-2M+L_{2}=L_1+L_2-2M\,</math></center> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Categoría:Problemas de inducción electromagnética (GIE)]] | [[Categoría:Problemas de inducción electromagnética (GIE)]] | ||
última version al 17:53 13 jun 2014
Contenido |
1 Enunciado
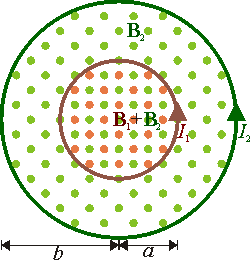
Dos solenoides cilíndricos muy largos se disponen concentricamente. Dichos solenoides poseen la misma longitud  y número de espiras N1 y N2, respectivamente, las cuales están arrolladas en el mismo sentido. Los radios de las bobinas son, respectivamente, a y b (a < b).
y número de espiras N1 y N2, respectivamente, las cuales están arrolladas en el mismo sentido. Los radios de las bobinas son, respectivamente, a y b (a < b).
- Determine la matriz de inducciones mutuas del sistema.
- Calcule la constante de acoplamiento entre las bobinas.
- Suponga que se conectan el extremo superior de la bobina interior con el extremo superior de la exterior. ¿Cuál es la autoinducción equivalente de la asociación?
2 Matriz de inducciones mutuas
Existen tres métodos a la hora de calcular los coeficientes de inducción mutua y autoinducción. Uno es el cálculo directo a partir de la fórmula de Neumann, que no consideraremos por ser extremadamente complicado. El segundo es partir del flujo inducido en cada solenoide por los campos magnéticos propios o ajenos. El tercero es a partir de la expresión de la energía magnética, que tampoco consideraremos aquí (puede encontrarse en esta versión extendida de este mismo problema
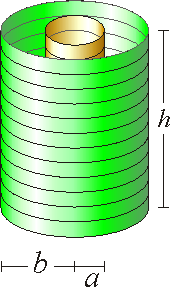
Es conocido que un solenoide muy largo de longitud h, radio R, con N espiras por las cuales circula una corriente I produce un campo magnético
- Si ρ < R
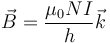
- Si ρ > R

En nuestro caso disponemos de dos solenoides, cada uno de los cuales crea su propio campo magnético. Por simple aplicación del principio de superposición resulta
- Si ρ < a
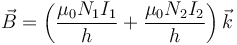
- Si a < ρ < b
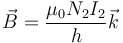
- Si b < ρ

donde I1, e I2 son las corrientes que circulan por los solenoides de radios a y b, respectivamente. Aquí hemos hecho uso de que todas las bobinas poseen la misma longitud y el mismo sentido de giro (lo que hace que todos los campos tengan el mismo sentido).
Para calcular los coeficientes de inducción mutua a partir de los flujos, partimos de las expresiones
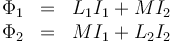
Si suponemos que I1 = 0, 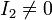 , sólo circula corriente por la bobina exterior, resultan los coeficientes M y L2. En este caso, el campo magnético vale
, sólo circula corriente por la bobina exterior, resultan los coeficientes M y L2. En este caso, el campo magnético vale
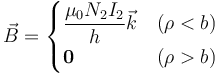
por lo que el flujo será el correspondiente a sumar las contribuciones de las Ni espiras que forman cada solenoide, teniendo en cuenta además la superficie de cada una de ellas, esto es
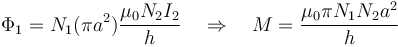
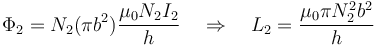
Aprovechando la simetría de los coeficientes, con el resultado anterior ya conocemos el coeficiente M, pero podemos hallarlos explícitamente empleando un razonamiento análogo.
Si es  , I2 = 0, a la hora de calcular el flujo sobre una bobina mayor, debe tenerse en cuenta que sólo hay campo dentro de la bobina que crea el campo, y es el área de ésta la que hay que considerar. Queda entonces
, I2 = 0, a la hora de calcular el flujo sobre una bobina mayor, debe tenerse en cuenta que sólo hay campo dentro de la bobina que crea el campo, y es el área de ésta la que hay que considerar. Queda entonces
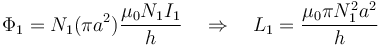
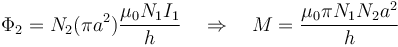
Finalmente, la matriz de inducciones mutuas es

Obsérvese como la simetría de la matriz resulta de aplicar razonamientos diferentes al elemento M (en un caso es el área la que está limitada, en el otro es el campo magnético).
3 Constante de acoplamiento
La constante de acoplamiento para un sistema de dos solenoides vale
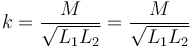
Sustituyendo los valores para este caso

Esta es siempre menor que la unidad pues en el cálculo de M hemos supuesto que  . Es igual a la unidad cuando
. Es igual a la unidad cuando  . En este caso, al tener las dos bobinas el mismo radio (aunque distinto número de espiras) todo el campo de una pasa por el interior de la otra y el acoplamiento es máximo
. En este caso, al tener las dos bobinas el mismo radio (aunque distinto número de espiras) todo el campo de una pasa por el interior de la otra y el acoplamiento es máximo
4 Asociación en serie
Cuando conectamos las dos bobinas, el sistema pasa a tener una sola entrada y una salida, y puede describirse por un solo coeficiente de autoinducción equivalente. Para hallar su valor, podemos
- Usar la expresión de la energía magnética
- Calcular el flujo magnético en el sistema
Si consideramos el sistema formado por las dos bobinas conectados por su extremo superior, el flujo magnético total a través de este sistema incluye los flujos a través de las N_1 espiras interiores y las N_2 exteriores. Pero teniendo en cuenta que la bobina exterior la recorremos en sentido contrario, la normal a las espiras exteriores va en sentido contrario a la normal de las interiores y por tanto


sustituyendo la relación entre los flujos y las intensidades

de donde obtenemos de nuevo la autoinducción equivalente