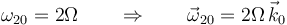Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Dos discos (Ex.Feb/14)

De Laplace

(Diferencias entre revisiones)
(→Solución alternativa)
(→Centros instantáneos (o permanentes) de rotación)
Línea 26: Línea 26:
</math></center>
</math></center>
-
Tener localizados los centros instantáneos de rotación nos permite relacionar las velocidades de cualquier punto (por ejemplo, <math>P\,</math>) con las correspondientes velocidades angulares:
+
Tener localizado el centro instantáneo o permanente de rotación de un movimiento plano (único punto con velocidad nula) nos permite relacionar la velocidad de un punto arbitrario (por ejemplo, <math>P\,</math>) y la velocidad angular correspondientes a dicho movimiento:
<center><math>
<center><math>
-
\vec{v}^{\, P}_{21}=\underbrace{\vec{v}^{\, I_{21}}_{21}}_{=\,\vec{0}}+\,\,\vec{\omega}_{21}\times\overrightarrow{I_{21}P}=\vec{\omega}_{21}\times\overrightarrow{CP} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
+
\vec{v}^{\, P}_{21}=\underbrace{\vec{v}^{\, C}_{21}}_{=\,\vec{0}}+\,\,\vec{\omega}_{21}\times\overrightarrow{CP}=\vec{\omega}_{21}\times\overrightarrow{CP} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
-
\vec{v}^{\, P}_{20}=\underbrace{\vec{v}^{\, I_{20}}_{20}}_{=\,\vec{0}}+\,\,\vec{\omega}_{20}\times\overrightarrow{I_{20}P}=\vec{\omega}_{20}\times\overrightarrow{AP} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
+
\vec{v}^{\, P}_{20}=\underbrace{\vec{v}^{\, A}_{20}}_{=\,\vec{0}}+\,\,\vec{\omega}_{20}\times\overrightarrow{AP}=\vec{\omega}_{20}\times\overrightarrow{AP} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
-
\vec{v}^{\, P}_{01}=\underbrace{\vec{v}^{\, I_{01}}_{01}}_{=\,\vec{0}}+\,\,\vec{\omega}_{01}\times\overrightarrow{I_{01}P}=\vec{\omega}_{01}\times\overrightarrow{OP}
+
\vec{v}^{\, P}_{01}=\underbrace{\vec{v}^{\, O}_{01}}_{=\,\vec{0}}+\,\,\vec{\omega}_{01}\times\overrightarrow{OP}=\vec{\omega}_{01}\times\overrightarrow{OP}
</math></center>
</math></center>

Revisión de 12:48 25 mar 2014

Contenido

[ocultar]

1 Enunciado

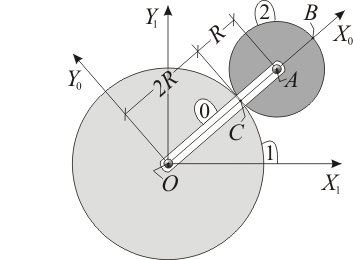
El disco móvil de centro A\, y radio R\, (sólido "2") rueda sin deslizar sobre el disco fijo de centro O\, y radio 2R\, (sólido "1"). Los centros de ambos discos se encuentran articulados a los extremos de una varilla (sólido "0") que rota con velocidad angular constante 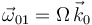\vec{\omega}_{01}=\Omega\,\vec{k}_0\, (ver figura).

  1. ¿Dónde se hallan los centros instantáneos (o permanentes) de rotación 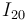I_{20}\, e I_{21}\,?
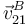
  2. Determine la velocidad instantánea \vec{v}^{B}_{21}\,
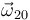
  3. Determine la velocidad angular \vec{\omega}_{20}\,


2 Centros instantáneos (o permanentes) de rotación

Se nos indica que el disco móvil (sólido "2") rueda sin deslizar sobre el disco fijo (sólido "1"). La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto entre ambos discos:

I_{21}\equiv C

Por otra parte, el centro del disco móvil (sólido "2") se halla articulado al extremo A\, de la varilla (sólido "0"). Por tanto, dicho punto A\, es un punto fijo (centro permanente de rotación) en el movimiento {20}:

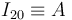
I_{20}\equiv A

Análogamente, el extremo O\, de la varilla (sólido "0") está articulado al centro del disco fijo (sólido "1"). Por tanto, dicho punto O\, es un punto fijo (centro permanente de rotación) en el movimiento {01}:

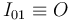
I_{01}\equiv O

Tener localizado el centro instantáneo o permanente de rotación de un movimiento plano (único punto con velocidad nula) nos permite relacionar la velocidad de un punto arbitrario (por ejemplo, P\,) y la velocidad angular correspondientes a dicho movimiento:

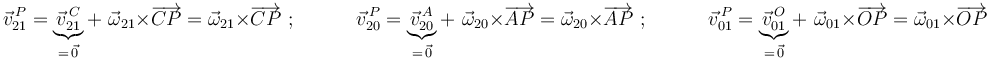
\vec{v}^{\, P}_{21}=\underbrace{\vec{v}^{\, C}_{21}}_{=\,\vec{0}}+\,\,\vec{\omega}_{21}\times\overrightarrow{CP}=\vec{\omega}_{21}\times\overrightarrow{CP} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}^{\, P}_{20}=\underbrace{\vec{v}^{\, A}_{20}}_{=\,\vec{0}}+\,\,\vec{\omega}_{20}\times\overrightarrow{AP}=\vec{\omega}_{20}\times\overrightarrow{AP} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}^{\, P}_{01}=\underbrace{\vec{v}^{\, O}_{01}}_{=\,\vec{0}}+\,\,\vec{\omega}_{01}\times\overrightarrow{OP}=\vec{\omega}_{01}\times\overrightarrow{OP}

3 Velocidad instantánea {21} de B

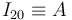Empezaremos calculando por composición de velocidades, la velocidad {21} del punto A\, (recuérdese que I_{20}\equiv A\,):

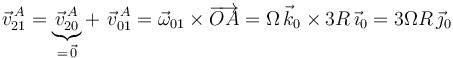
\vec{v}^{\, A}_{21}=\underbrace{\vec{v}^{\, A}_{20}}_{=\,\vec{0}}+\,\,\vec{v}^{\, A}_{01}=\vec{\omega}_{01}\times\overrightarrow{OA}=\Omega\,\vec{k}_0\times 3R\,\vec{\imath}_0=3\Omega R\,\vec{\jmath}_0

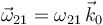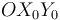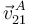A continuación, deducimos el valor de \vec{\omega}_{21}=\omega_{21}\,\vec{k}_0\, (dirección obligada para un movimiento plano paralelo a OX_0Y_0\,) a partir de su necesaria relación con \vec{v}^{\, A}_{21}\,:

\vec{v}^A_{21}=\vec{\omega}_{21}\,\times\,\overrightarrow{CA}\,\,\,\,\,\Longrightarrow\,\,\,\,\,3\Omega R\,\vec{\jmath}_0=\omega_{21}\,\vec{k}_0\,\times\, R\,\vec{\imath}_0\,\,\,\,\,\Longrightarrow\,\,\,\,\,3\Omega R\,\vec{\jmath}_0=\omega_{21} R\,\vec{\jmath}_0\,\,\,\,\,\Longrightarrow\,\,\,\,\,\omega_{21}=3\Omega\,\,\,\,\,\Longrightarrow\,\,\,\,\,\vec{\omega}_{21}=3\Omega\,\vec{k}_0

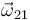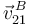Y conocida \vec{\omega}_{21}\,, es ya inmediato el cálculo de \vec{v}^{\, B}_{21}\,:

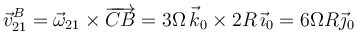
\vec{v}^B_{21}=\vec{\omega}_{21}\times\overrightarrow{CB}=3\Omega\,\vec{k}_0\times 2R\,\vec{\imath}_0=6\Omega R\vec{\jmath}_0

4 Velocidad angular {20}

La velocidad angular del movimiento {20} la podemos obtener fácilmente a partir de la ley de composición de velocidades angulares:

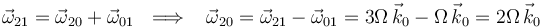
\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\,\,\,\,\Longrightarrow\,\,\,\,\,\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}=3\Omega\,\vec{k}_0-\Omega\,\vec{k}_0=2\Omega\,\vec{k}_0

5 Solución alternativa (más larga)

5.1 Velocidad instantánea {21} de B

De acuerdo con la ecuación del campo de velocidades:

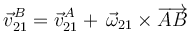
\vec{v}^B_{21}=\vec{v}^A_{21}+\,\vec{\omega}_{21}\times\overrightarrow{AB}

Si esta misma ecuación la aplicamos al punto C, cuya velocidad en el movimiento {21} sabemos que es nula:

\vec{0}=\vec{v}^C_{21}=\vec{v}^A_{21}+\,\vec{\omega}_{21}\times\overrightarrow{AC}

pero C es el punto diametralmente opuesto a B:

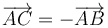
\overrightarrow{AC}=-\overrightarrow{AB}

lo que nos da:

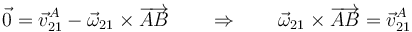
\vec{0}=\vec{v}^A_{21}-\vec{\omega}_{21}\times\overrightarrow{AB}\qquad\Rightarrow\qquad \vec{\omega}_{21}\times\overrightarrow{AB}=\vec{v}^A_{21}

que llevado a la ecuación para la velocidad de B nos da:

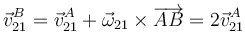
\vec{v}^B_{21}=\vec{v}^A_{21}+\vec{\omega}_{21}\times\overrightarrow{AB}=2\vec{v}^A_{21}

Necesitamos hallar la velocidad del centro del disco "2". Aplicando la ley de composición de velocidades:

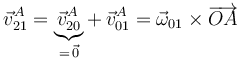
\vec{v}^A_{21}=\underbrace{\vec{v}^A_{20}}_{=\,\vec{0}} +\, \vec{v}^A_{01}=\vec{\omega}_{01}\times\overrightarrow{OA}

De aquí:

\vec{v}^B_{21}=2\,\vec{\omega}_{01}\times\overrightarrow{OA}=\left(2\Omega\,\vec{k}_0\right)\times\left((2R+R)\,\vec{\imath}_0\right)=6\Omega R\,\vec{\jmath}_0

5.2 Velocidad angular {20}

La velocidad angular del movimiento {20} la podemos obtener recurriendo de nuevo a que los discos ruedan sin deslizar uno sobre otro y por tanto el punto C es el CIR del movimiento {20}. Por la ley de composición de velocidades:

\vec{0}=\vec{v}^{\, C}_{21}=\vec{v}^{\, C}_{20}+\vec{v}^{\, C}_{01}

siendo la velocidad relativa:

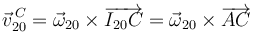
\vec{v}^{\, C}_{20}=\vec{\omega}_{20}\times\overrightarrow{I_{20}C}=\vec{\omega}_{20}\times\overrightarrow{AC}

que expresada en componentes da:

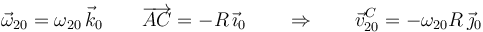
\vec{\omega}_{20}=\omega_{20}\,\vec{k}_0\qquad \overrightarrow{AC}=-R\,\vec{\imath}_0\qquad\Rightarrow\qquad \vec{v}^C_{20}=-\omega_{20}R\,\vec{\jmath}_0

Por su parte, la velocidad de arrastre vale:

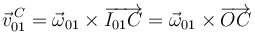
\vec{v}^{\, C}_{01}=\vec{\omega}_{01}\times\overrightarrow{I_{01}C}=\vec{\omega}_{01}\times\overrightarrow{OC}

que expresada en componentes es:

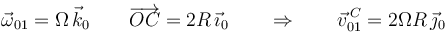
\vec{\omega}_{01}=\Omega\,\vec{k}_0\qquad \overrightarrow{OC}=2R\,\vec{\imath}_0\qquad\Rightarrow\qquad \vec{v}^{\, C}_{01}=2\Omega R\,\vec{\jmath}_0

Llevando estas dos expresiones a la velocidad absoluta nos queda:

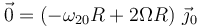
\vec{0}=\left(-\omega_{20}R+2\Omega R\right)\,\vec{\jmath}_0

y por tanto:

\omega_{20}=2\Omega\qquad\Rightarrow\qquad \vec{\omega}_{20}=2\Omega\,\vec{k}_0
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Dos_discos_(Ex.Feb/14)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace