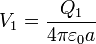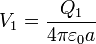Dos esferas conductoras conectadas
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Solución) |
||
| Línea 7: | Línea 7: | ||
<center>[[Imagen:dosesferashilo.png]]</center> | <center>[[Imagen:dosesferashilo.png]]</center> | ||
==Solución== | ==Solución== | ||
| + | ===Carga en cada esfera=== | ||
| + | Al estar muy alejadas, las dos esferas se comportan como conductores independientes, salvo por el hecho de que están conectadas por un hilo. Este hilo, al ser ideal, no añade capacidad ni carga al sistema, pero garantiza que ambas esferas estén al mismo potencial, ya que las cargas pueden moverse de una esfera a la otra. | ||
| + | |||
| + | El potencial en cada una de las esferas será, en función de su carga | ||
| + | <center> | ||
| + | <math>V_1 = \frac{Q_1}{4\pi\varepsilon_0 a}</math>{{qquad}}{{qquad}}<math>V_1 = \frac{Q_1}{4\pi\varepsilon_0 a}</math></center> | ||
| + | |||
| + | ===Densidad de carga y campo=== | ||
| + | |||
[[Categoría:Problemas de campo eléctrico en presencia de conductores]] | [[Categoría:Problemas de campo eléctrico en presencia de conductores]] | ||
Revisión de 10:02 2 dic 2008
Contenido |
1 Enunciado
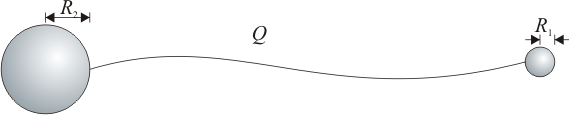
Se tiene un conductor formado por dos esferas de radios a y b (a < b), muy alejadas entre sí (de forma que la influencia de una sobre la otra es despreciable), pero unidas por un cable conductor ideal. El conductor almacena una carga Q.
- ¿Cuánta carga se va a cada esfera? ¿En cuál de las dos es mayor la carga almacenada?
- ¿En cual de las dos esferas es mayor la densidad de carga? ¿Y el campo eléctrico en la superficie?
2 Solución
2.1 Carga en cada esfera
Al estar muy alejadas, las dos esferas se comportan como conductores independientes, salvo por el hecho de que están conectadas por un hilo. Este hilo, al ser ideal, no añade capacidad ni carga al sistema, pero garantiza que ambas esferas estén al mismo potencial, ya que las cargas pueden moverse de una esfera a la otra.
El potencial en cada una de las esferas será, en función de su carga