Masa que cae sobre resorte
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 14: | Línea 14: | ||
Si la colisión es perfectamente elástica, | Si la colisión es perfectamente elástica, | ||
<ol style="list-style-type:lower-alpha" start="3"> | <ol style="list-style-type:lower-alpha" start="3"> | ||
| - | <li> Calcule la nueva altura que alcanza la masa | + | <li> Calcule la nueva altura que alcanza la masa <math>m_1</math> tras la colisión.</li> |
<li> Calcule cuánto es el máximo que se comprime el resorte por efecto del golpe en la plataforma.</li> | <li> Calcule cuánto es el máximo que se comprime el resorte por efecto del golpe en la plataforma.</li> | ||
</ol> | </ol> | ||
| Línea 23: | Línea 23: | ||
</ol> | </ol> | ||
Tómese <math>g=9.8\,\mathrm{m}/\mathrm{s}^2</math>. | Tómese <math>g=9.8\,\mathrm{m}/\mathrm{s}^2</math>. | ||
| + | |||
==Compresión del resorte== | ==Compresión del resorte== | ||
==Velocidad de impacto== | ==Velocidad de impacto== | ||
Revisión de 18:27 27 ene 2014
Contenido |
1 Enunciado
Se tiene una plataforma de masa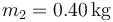 
situada sobre un resorte de constante 
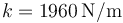y longitud natural 
.
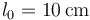- Calcule cuánto se comprime el resorte debido al peso de la masa, en la posición de equilibrio.
Sobre esta plataforma se deja caer una masa 
, soltándola sin velocidad inicial desde una altura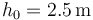 
sobre la plataforma
- Calcule la velocidad que tiene la masa $m_1$ justo antes de impactar con la plataforma.
Si la colisión es perfectamente elástica,
- Calcule la nueva altura que alcanza la masa m1 tras la colisión.
- Calcule cuánto es el máximo que se comprime el resorte por efecto del golpe en la plataforma.
Si la colisión, en vez de ser elástica, es completamente inelástica,
- ¿Cuánta energía se pierde en la colisión?
- ¿Cuánto se comprime como máximo el resorte tras la colisión?
Tómese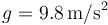 
.
