Cadena que cae de una mesa
De Laplace
(→Solución) |
(→Solución) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 33: | Línea 33: | ||
Para hallar la solución de esta ecuación buscamos aquellas funciones cuyas segundas derivadas son iguales a ellas mismas multiplicadas por una constante. Estas son las exponenciales. Si tenemos una solución de la forma | Para hallar la solución de esta ecuación buscamos aquellas funciones cuyas segundas derivadas son iguales a ellas mismas multiplicadas por una constante. Estas son las exponenciales. Si tenemos una solución de la forma | ||
| - | <center><math>s_1 = \mathrm{e}^{\lambda t}</math></center> | + | <center><math>s_1 = \mathrm{e}^{\lambda t}\,</math></center> |
al sustituir queda | al sustituir queda | ||
| Línea 49: | Línea 49: | ||
y que parte del reposo, <math>\dot{s}(t=0)=0</math>. | y que parte del reposo, <math>\dot{s}(t=0)=0</math>. | ||
| - | <center><math>0 =\dot{s}_0 = \left.c_1\sqrt{\frac{g}{L}\mathrm{e}^{t\sqrt{g/L}}-c_2\sqrt{\frac{g}{L}}\mathrm{e}^{-t\sqrt{g/L}}\right|_{t=0}=\sqrt{\frac{g}{L}}(c_1-c_2)</math></center> | + | <center><math>0 =\dot{s}_0 = \left. c_1\sqrt{\frac{g}{L}}\mathrm{e}^{t\sqrt{g/L}}-c_2\sqrt{\frac{g}{L}}\mathrm{e}^{-t\sqrt{g/L}}\right|_{t=0}=\sqrt{\frac{g}{L}}(c_1-c_2)</math></center> |
La solución de este sistema de ecuaciones es | La solución de este sistema de ecuaciones es | ||
| Línea 59: | Línea 59: | ||
<center><math>s(t) = s_0\frac{\mathrm{e}^{t\sqrt{g/L}}+\mathrm{e}^{-t\sqrt{g/L}}}{2}</math></center> | <center><math>s(t) = s_0\frac{\mathrm{e}^{t\sqrt{g/L}}+\mathrm{e}^{-t\sqrt{g/L}}}{2}</math></center> | ||
| - | Esta fracción es una función con nombre | + | Esta fracción es una función con nombre propio: se denomina el coseno hiperbólico |
<center><math>s(t) = s_0\cosh\left(\sqrt{\frac{g}{L}}t\right)</math></center> | <center><math>s(t) = s_0\cosh\left(\sqrt{\frac{g}{L}}t\right)</math></center> | ||
última version al 15:12 22 ene 2014
1 Enunciado
Suponga una mesa horizontal sin rozamiento sobre la cual se halla una cadena de longitud L y masa M distribuida uniformemente. Esta cadena está estirada de forma que una parte de ella, de longitud s, pende por el lateral de la mesa. Esta parte colgante tira del resto, por lo que la cadena empieza a resbalar por la mesa cayendo aceleradamente.
Determine la aceleración de los puntos de la cadena como función de s. Si inicialmente sobresale una cantidad s0 y la velocidad inicial es nula, ¿cómo varía s con el tiempo mientras resbala la cadena?
2 Solución
Este problema es realmente de dinámica d eun sistema de partícula, ya que describe el comportamiento no solo de una o dos masas,sino de un conjunto de muchas de ellas. No obstante, su solución es una consecuencia directa del problema de dos masas una de las cuales se encuentra sobre un plano y la otra cae verticalmente por su lado.
Tal como se ve en la solución de ese problema, el módulo de la aceleración con la que se desliza una masa y cae la otra es

siendo m2 la masa que cuelga y m1 la situada sobre el plano horizontal.
En este problema, m2 es la masa del trozo de cadena que cuelga y m1 la del trozo sobre la mesa. la suma de las dos es la masa total de la cadena
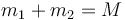
La masa que cuelga va variando, ya que depende de cuanta cadena ha sobrepasado el borde la mesa. Si en un instante dado hay una porción s colgando, podemos establecer la proporcionalidad
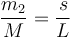
y por tanto la ecuación para la aceleración queda
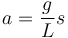
Por otro lado la aceleración es la segunda derivada de la posición respecto al tiempo, estando la posición del extremo de la cadena dada justamente pors. Por tanto, queda la ecuación de movimiento
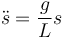
Para hallar la solución de esta ecuación buscamos aquellas funciones cuyas segundas derivadas son iguales a ellas mismas multiplicadas por una constante. Estas son las exponenciales. Si tenemos una solución de la forma
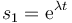
al sustituir queda
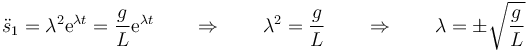
Tenemos dos posibilidades para el exponente. La solución general será una combinación de ambas
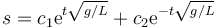
Los valores de c1 y c2 los obtenemos de las condiciones iniciales. Sabemos que en t=0, s = s0
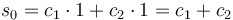
y que parte del reposo, 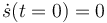 .
.
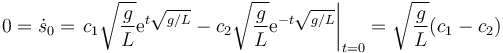
La solución de este sistema de ecuaciones es

y por tanto la solución del problema es
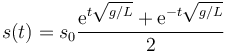
Esta fracción es una función con nombre propio: se denomina el coseno hiperbólico

Esta función comienza con tangente horizontal (velocidad nula) pero crece rápidamente, lo que indica que la cadena cae cada vez más rápidamente, con una aceleración creciente.





