Primera Prueba de Control 2012/13 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(→Partícula con movimiento rectilíneo) |
(→Partícula con movimiento rectilíneo) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==[[Partícula con movimiento rectilíneo, Noviembre 2012 (G.I.C.) | Partícula con movimiento rectilíneo]]== | ==[[Partícula con movimiento rectilíneo, Noviembre 2012 (G.I.C.) | Partícula con movimiento rectilíneo]]== | ||
| + | Una partícula realiza un movimiento unidimensional, de modo que su | ||
| + | velocidad y aceleración cumplen la relación <math>a(t)\,v(t) = 3C^2t^2/2</math>, | ||
| + | siendo <math>C</math> una constante. | ||
| + | #¿Cuales son las dimensiones de la constante <math>C</math>? | ||
| + | #Si la velocidad inicial es <math>v(0)=v_0</math>, ¿cuál es la expresión de la velocidad en cualquier instante de tiempo? | ||
| + | #Supongamos que <math>v_0=0</math> y la posición inicial de la partícula es <math>x(0)=0</math>. ¿Cuál es la posición de la partícula en cualquier instante de tiempo? | ||
==[[Barra articulada en otra barra, Noviembre 2012 (G.I.C.) | Barra articulada en otra barra]]== | ==[[Barra articulada en otra barra, Noviembre 2012 (G.I.C.) | Barra articulada en otra barra]]== | ||
| + | [[Imagen:F1_GIC_PPC_doble_barra_enunciado.png|right]] | ||
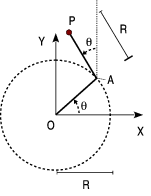
| + | Una barra de radio <math>R</math> gira alrededor de uno de sus extremos, situado en el punto <math>O</math>. En su otro extremo se articula otra barra de longitud <math>R</math> que a su vez gira en con la misma velocidad angular. | ||
| + | |||
| + | #Expresa el vector de posición <math>\overrightarrow{OP}</math> en función del ángulo <math>\theta</math> de la figura. | ||
| + | #Si <math>\dot{\theta}=\omega</math> y el módulo de la velocidad del punto <math>P</math> es <math>v_0</math>, encuentra el valor de <math>\omega</math>. | ||
| + | #Calcula el vector normal en cada punto de la trayectoria de <math>P</math>. | ||
| + | #Calcula la curvatura en cada punto de la trayectoria. | ||
| + | |||
| + | ==[[Dos masas en un triángulo, Noviembre 2012 (G.I.C.) | Dos masas en un triángulo]]== | ||
| + | [[Imagen:F1_GIC_PPC_triangulo_enunciado.png|right]] | ||
| + | Se tienen dos masas de magnitud M=100g situadas a una distancia d=10cm. Otra masa m=10g se sitúa en el vértice superior del triángulo equilátero de la figura. Calcula el módulo de la fuerza gravitatoria sobre la masa m. | ||
última version al 19:38 14 ene 2014
1 Partícula con movimiento rectilíneo
Una partícula realiza un movimiento unidimensional, de modo que su
velocidad y aceleración cumplen la relación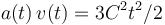 
,
siendo C una constante.
- ¿Cuales son las dimensiones de la constante C?
- Si la velocidad inicial es v(0) = v0, ¿cuál es la expresión de la velocidad en cualquier instante de tiempo?
- Supongamos que v0 = 0 y la posición inicial de la partícula es x(0) = 0. ¿Cuál es la posición de la partícula en cualquier instante de tiempo?
2 Barra articulada en otra barra
Una barra de radio R gira alrededor de uno de sus extremos, situado en el punto O. En su otro extremo se articula otra barra de longitud R que a su vez gira en con la misma velocidad angular.
- Expresa el vector de posición
en función del ángulo θ de la figura.
- Si
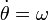y el módulo de la velocidad del punto P es v0, encuentra el valor de ω.
- Calcula el vector normal en cada punto de la trayectoria de P.
- Calcula la curvatura en cada punto de la trayectoria.
3 Dos masas en un triángulo
Se tienen dos masas de magnitud M=100g situadas a una distancia d=10cm. Otra masa m=10g se sitúa en el vértice superior del triángulo equilátero de la figura. Calcula el módulo de la fuerza gravitatoria sobre la masa m.
