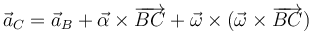Deslizamiento de una placa triangular

De Laplace

(Diferencias entre revisiones)

Revisión de 12:02 12 ene 2014

Contenido

1 Enunciado
2 Introducción
3 Velocidad de los vértices
- 3.1 Posiciones de los vértices
- 3.2 Velocidades
4 Velocidad angular
5 Tipo de movimiento
6 Eje instantáneo de rotación
7 Aceleración de cada vértice
- 7.1 A partir del campo de aceleraciones
8 Propiedades del CM

1 Enunciado

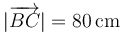Una placa en forma de triángulo rectángulo con catetos que miden $|\overrightarrow{AB}|=60\,\mathrm{cm}$ y $|\overrightarrow{BC}|=80\,\mathrm{cm}$ desliza por dos paredes (XZ e YZ) y el suelo (XY) de forma que:

Su vértice C desciende por la esquina entre las dos paredes (eje Z)
Su vértice B se desliza por la esquina entre la pared del fondo y el suelo (eje Y).
Su vértice A se desliza por el suelo, de forma que el vector de posición relativa 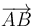$\overrightarrow{AB}$ es siempre paralelo a la esquina entre la pared lateral y el suelo.

Suponga que la velocidad del vértice B es constante, 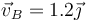$\vec{v}_B=1.2\vec{\jmath}$ (m/s)

En un determinado momento, el vértice B se encuentra a 64\,cm de la esquina. Para este instante:

Calcule la velocidad de cada vértice.
Halle la velocidad angular de la placa.
Identifique el tipo de movimiento que describe el sólido (traslación, rotación,…)
Dé la ecuación del EIRMD (o EIR, en su caso).
Halle la aceleración de cada vértice.
El centro de masas, G, de un triángulo homogéneo es el baricentro, cuyas coordenadas son la media aritmética de las de los tres vértices. Calcule la velocidad y aceleración del CM para este mismo instante. ¿Qué trayectoria describe el baricentro?

2 Introducción

Este problema es prácticamente idéntico, salvo en el cálculo de la aceleración, al problema “deslizamiento de una barra”. Como en ese tenemos un movimiento en el que conocemos la velocidad de un punto que se mueve horizontalmente, y queremos hallar la de uno que se mueve verticalmente.

Lo único que se añade es el aspecto tridimensional del problema, pero dado que el punto A se desplaza como el B, en realidad esto es un movimiento plano, siendo el plano director el YZ.

Como en el problema citado, para cada apartado existen diferentes formas correctas de llegar a cada resultado.

En todo lo que sigue usamos el SI, por lo que aunque no se indiquen unidades, se entiende que las distancias se miden en m, las velocidades en m/s, las aceleraciones en m/s², la velocidad angular en rad/s y la aceleración angular en rad/s².

3 Velocidad de los vértices

3.1 Posiciones de los vértices

Antes de calcular las velocidades, vamos a determinar las posiciones de cada uno de los vértices en el instante en cuestión.

El vértice B está sobre el eje OY, a una distancia de 64 cm de la esquina. Si tomamos el origen de coordenadas en la esquina y

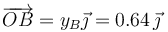
$\overrightarrow{OB}=y_B\vec{\jmath}=0.64\,\vec{\jmath}$

El punto A se mueve paralelamente al B, sobre una recta a 60 cm de este. Por ello

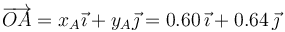
$\overrightarrow{OA}=x_A\vec{\imath}+y_A\vec{\jmath}=0.60\,\vec{\imath}+0.64\,\vec{\jmath}$

El vértice C está sobre el eje Z.

$\overrightarrow{OC}=z_C\vec{k}$

La altura instantánea la podemos hallar mediante el teorema de Pitágoras. si h es la longitud del cateto BC

$z_c = \sqrt{h^2-y_B^2}=\sqrt{0.80^2-0.64^2}=0.48$

En forma vectorial

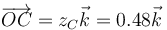
$\overrightarrow{OC}=z_C\vec{k}=0.48\vec{k}$

3.2 Velocidades

Tenemos como dato la velocidad del vértice B

$\vec{v}_B=\dot{y}_B\vec{\jmath}=1.2\,\vec{\jmath}$

y puesto que nos dicen que el lado AB es paralelo en todo momento al eje OX, esto implica que A se mueve con la misma velocidad que B

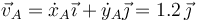
$\vec{v}_A=\dot{x}_A\vec{\imath}+\dot{y}_A\vec{\jmath}=1.2\,\vec{\jmath}$

Para hallar la velocidad del vértice C tenemos varios métodos, como los descritos en el problema citado

A partir de la condición de rigidez.
A partir del campo de velocidades.
Derivando la posición como función del tiempo.
A partir del eje instantáneo de rotación.

Aquí describiremos solamente el método del campo de velocidades. Los otros pueden consultarse en el otro problema.

Tenemos, que para cualquier punto del sólido se cumple

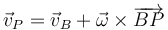
$\vec{v}_P=\vec{v}_B+\vec{\omega}\times\overrightarrow{BP}$

En particular, P puede ser el punto A. Ahora bien, se cumple

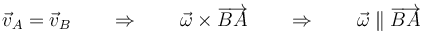
$\vec{v}_A=\vec{v}_B\qquad\Rightarrow\qquad \vec{\omega}\times\overrightarrow{BA}\qquad\Rightarrow\qquad \vec{\omega}\parallel\overrightarrow{BA}$

En el momento que tenemos dos puntos con la misma velocidad lineal, ya sabemos que la velocidad angular va a ser paralela a la recta que pasa por esos dos puntos, es decir,

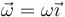
$\vec{\omega}=\omega\vec{\imath}$

Si ahora aplicamos la misma fórmula al punto C tenemos

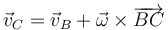
$\vec{v}_C=\vec{v}_B+\vec{\omega}\times\overrightarrow{BC}$

siendo

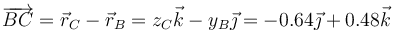
$\overrightarrow{BC}=\vec{r}_C-\vec{r}_B=z_C\vec{k}-y_B\vec{\jmath}= -0.64\vec{\jmath}+0.48\vec{k}$

Poniendo cada vector en sus componentes cartesianas

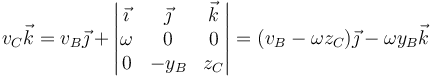
$v_C\vec{k}=v_B\vec{\jmath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega & 0 & 0 \\ 0 & -y_B & z_C\end{matrix}\right| = (v_B-\omega z_C)\vec{\jmath}-\omega y_B\vec{k}$

Igualamos componente a componente y queda

$0 = v_B-\omega z_C \qquad\qquad v_C = -\omega y_B$

De aquí calculamos a la vez la velocidad angular y la velocidad del vértice C

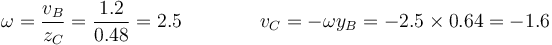
$\omega = \frac{v_B}{z_C}=\frac{1.2}{0.48}=2.5\qquad\qquad v_C = -\omega y_B = -2.5\times 0.64 = -1.6$

En forma vectorial

$\vec{\omega}=2.5\vec{\imath}\qquad\qquad \vec{v}_C=-1.6\vec{k}$

4 Velocidad angular

La velocidad angular la acabamos de calcular

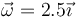
$\vec{\omega}=2.5\vec{\imath}$

5 Tipo de movimiento

En el momento en que la velocidad angular no es nula, ya el movimiento solo puede ser una rotación o uno helicoidal. Para distinguir entre ellos, calculamos la velocidad de deslizamiento, que es la misma para todos los puntos

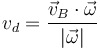
$v_d = \frac{\vec{v}_B\cdot\vec{\omega}}{|\vec{\omega}|}$

pero al ser vectores perpendiculares

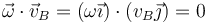
$\vec{\omega}\cdot\vec{v}_B=(\omega\vec{\imath})\cdot(v_B\vec{\jmath})=0$

la velocidad de deslizamiento es nula ( $v d = 0$ ). Por tanto el movimiento es una rotación pura.

6 Eje instantáneo de rotación

La ecuación del eje respecto al punto B la calculamos mediante la fórmula general

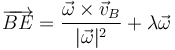
$\overrightarrow{BE}=\frac{\vec{\omega}\times\vec{v}_B}{|\vec{\omega}|^2}+\lambda\vec{\omega}$

Un punto del eje nos lo da el primer término

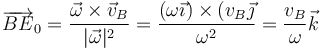
$\overrightarrow{BE}_0=\frac{\vec{\omega}\times\vec{v}_B}{|\vec{\omega}|^2}=\frac{(\omega\vec{\imath})\times(v_B\vec{\jmath}}{\omega^2}=\frac{v_B}{\omega}\vec{k}$

pero, sustituyendo la ecuación que nos da el valor de ω, queda

$\overrightarrow{BE}_0=z_C\vec{k}$

Numéricamente

$\overrightarrow{BE}_0=\frac{\vec{\omega}\times\vec{v}_B}{|\vec{\omega}|^2}=\frac{(2.5\vec{\imath})\times(1.2\vec{\jmath}}{2.5^2}=0.48\vec{k}$

Por tanto la ecuación vectorial del eje es

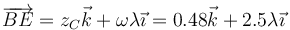
$\overrightarrow{BE}=z_C\vec{k}+\omega\lambda\vec{\imath}=0.48\vec{k}+2.5\lambda\vec{\imath}$

Si la escribimos respecto al origen de coordenadas

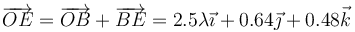
$\overrightarrow{OE}=\overrightarrow{OB}+\overrightarrow{BE}=2.5\lambda\vec{\imath}+0.64\vec{\jmath}+0.48\vec{k}$

Esto lo podemos separar en sus componentes cartesianas

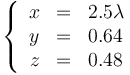
$\left\{\begin{array}{rcl} x & = & 2.5\lambda \\ y & = & 0.64 \\ z & = & 0.48\end{array}\right.$

Como en el problema de la barra, el eje es una recta perpendicular al plano de movimiento, situado sobre el punto donde cortan las perpendiculares a las dos velocidades, que es la esquina opuesta del rectángulo que pasa por C, O y B

7 Aceleración de cada vértice

La aceleración del vértice B es un dato. Puesto que se mueve a velocidad constante

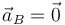
$\vec{a}_B=\vec{0}$

El punto A también se mueve uniformemente, puesto que siempre se mantiene en la misma posición relativa respecto a B

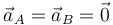
$\vec{a}_A=\vec{a}_B=\vec{0}$

Para hallar la aceleración del vértice C, de nuevo tenemos diferentes formas de hacerlo, siendo las más directas:

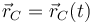
Derivando dos veces la ecuación horaria $\vec{r}_C=\vec{r}_C(t)$ .
A partir del campo de aceleraciones de un sólido.

7.1 A partir del campo de aceleraciones

La expresión para la aceleración de C se puede calcular mediante la expresión

$\vec{a}_C=\vec{a}_B+\vec{\alpha}\times\overrightarrow{BC}+\vec{\omega}\times(\vec{\omega}\times\overrightarrow{BC})$

8 Propiedades del CM

@@ Línea 161: / Línea 161: @@
 <center><math>\vec{a}_A=\vec{a}_B=\vec{0}</math></center>
+Para hallar la aceleración del vértice C, de nuevo tenemos diferentes formas de hacerlo, siendo las más directas:
+* Derivando dos veces la ecuación horaria <center><math>\vec{r}_C=\vec{r}_C(t)</math></center>.
+* A partir del campo de aceleraciones de un sólido.
+===A partir del campo de aceleraciones===
+La expresión para la aceleración de C se puede calcular mediante la expresión
+<center><math>\vec{a}_C=\vec{a}_B+\vec{\alpha}\times\overrightarrow{BC}+\vec{\omega}\times(\vec{\omega}\times\overrightarrow{BC})</math></center>
 ==Propiedades del CM==
 [[Categoría:Problemas de cinemática del sólido rígido (GIE)]]

Deslizamiento de una placa triangular

De Laplace

Revisión de 12:02 12 ene 2014

Contenido

1 Enunciado

2 Introducción

3 Velocidad de los vértices

3.1 Posiciones de los vértices

3.2 Velocidades

4 Velocidad angular

5 Tipo de movimiento

6 Eje instantáneo de rotación

7 Aceleración de cada vértice

7.1 A partir del campo de aceleraciones

8 Propiedades del CM

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES