CIR de una bicicleta (G.I.A.)
De Laplace
(Página creada con '== Enunciado == right Los radios de las ruedas delantera (sólido "2") y trasera (sólido "0") de un velocípedo son <math>R</math> y <…') |
(→Movimiento {20}) |
||
| Línea 41: | Línea 41: | ||
el teorema de los tres centros. En la figura puede observarse como | el teorema de los tres centros. En la figura puede observarse como | ||
<math>I_{01}</math>, <math>I_{03}</math> e <math>I_{31}</math> están alineados, así como <math>I_{21}</math>, <math>I_{23}</math> e <math>I_{31}</math>. | <math>I_{01}</math>, <math>I_{03}</math> e <math>I_{31}</math> están alineados, así como <math>I_{21}</math>, <math>I_{23}</math> e <math>I_{31}</math>. | ||
| + | |||
| + | [[Categoría: Problemas de movimiento plano]] | ||
última version al 16:21 10 ene 2014
Contenido |
1 Enunciado
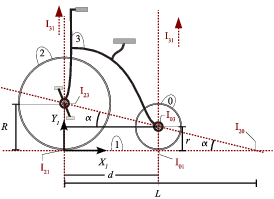
Los radios de las ruedas delantera (sólido "2") y trasera (sólido "0") de un velocípedo son R y r, respectivamente (R > r); y los puntos de contacto de aquéllas con el suelo (sólido "1") están separados una distancia d. Determinar gráficamente la posición del C.I.R. del movimiento {20}, sabiendo que las dos ruedas del velocípedo ruedan sin deslizar sobre el suelo.
2 Solución
Vamos a usar el teorema de los tres centros para encontrar el punto I20. Para ello buscamos el CIR de cada uno de los movimientos del sistema
2.1 Movimiento {21}
La rueda gira sin deslizar, por tanto el punto de contacto es el punto I21.
2.2 Movimiento {01}
La rueda gira sin deslizar, por tanto el punto de contacto es el punto I01.
2.3 Movimiento {23}
Respecto al velocípedo, la rueda gira alrededor de su centro, que resulta ser el punto I23.
2.4 Movimiento {03}
Respecto al velocípedo, la rueda gira alrededor de su centro, que resulta ser el punto I03.
2.5 Movimiento {20}
De la composición {20}={21}+{10}, el CIR I20 debe estar en la línea que une I21 e I01. Y de la composición {20}={23}+{30}, el CIR I20 debe estar en la línea que une I23 e I03. El punto de corte de estas dos líneas determina la posición de I20. De la figura vemos que

Si consideramos el origen del triedro "1" en I21, el vector de posición de I20 es
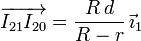
Observemos que al generalizar el concepto de CIR a una traslación colocando el CIR en el infinito, podemos incluir las traslaciones en el teorema de los tres centros. En la figura puede observarse como I01, I03 e I31 están alineados, así como I21, I23 e I31.