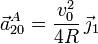Barra horizontal sobre un disco (G.I.A.)

De Laplace

(Diferencias entre revisiones)

última version al 17:20 10 ene 2014

Contenido

1 Enunciado
2 Solución

1 Enunciado

El sistema de la figura consta de un disco (sólido "0"), de centro $O$ y radio $R$ , que rueda sin deslizar sobre el eje horizontal $O 1 X 1$ del triedro fijo $O 1 X 1 Y 1$ (sólido "1"); y de una barra de longitud indefinida (sólido "2"), que se desplaza horizontalmente con velocidad constante $v 0$ , manteniéndose siempre en contacto tangente con el perímetro del disco (punto $A$ ) y sin deslizar sobre éste. Halla:

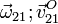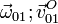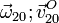Las reducciones cinemáticas de los movimientos {21}, {01} y {20} en el centro del disco (punto $O$ ), es decir: ${\vec{\omega}_{21};\vec{v}_{21}^O}$ , ${\vec{\omega}_{01};\vec{v}_{01}^O}$ y ${\vec{\omega}_{20};\vec{v}_{20}^O}$ .
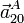La aceleración relativa barra-disco del punto de contacto $A$ , es decir, $\vec{a}_{20}^A$ .

2 Solución

Analicemos cada uno de los movimientos.

2.1 Movimiento {21}

Esta es una traslación pura, con velocidad uniforme $\vec{v}_{21}=v_0\,\vec{\imath}_1$ . La reducción en cualquier punto es

$\vec{\omega}_{21}=\vec{0}\qquad\qquad\vec{v}_{21}=v_0\,\vec{\imath}_1$

En particular

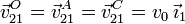
$\vec{v}_{21}^O=\vec{v}_{21}^A=\vec{v}_{21}^C=v_0\,\vec{\imath}_1$

2.2 Movimiento {01}

El disco rueda sin deslizar sobre el eje $O 1 X 1$ . Por tanto el punto de contacto $C$ es el CIR, y la reducción en él es

$\vec{\omega}_{01}=\omega_{01}\,\vec{k}\qquad\qquad\vec{v}_{01}^C=\vec{0}$

Necesitaremos también las velocidades en $O$ y $A$ . Usando la ecuación del campo de velocidades

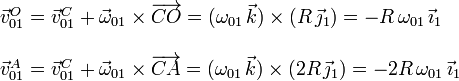
$\begin{array}{l} \vec{v}_{01}^O=\vec{v}_{01}^C+\vec{\omega}_{01}\times\overrightarrow{CO}=(\omega_{01}\,\vec{k})\times(R\,\vec{\jmath}_1) = -R\,\omega_{01}\,\vec{\imath}_1\\ \\ \vec{v}_{01}^A=\vec{v}_{01}^C+\vec{\omega}_{01}\times\overrightarrow{CA}=(\omega_{01}\,\vec{k})\times(2R\,\vec{\jmath}_1) = -2R\,\omega_{01}\,\vec{\imath}_1 \end{array}$

2.3 Movimiento {20}

Como la barra no desliza sobre el disco, la velocidad relativa del punto de contacto es nula, por lo que $A$ es el CIR del movimiento. La reducción en $A$ es

$\vec{\omega}_{20}=\omega_{20}\,\vec{k}\qquad\qquad\vec{v}_{20}^A=\vec{0}$

La velocidad en $O$ sería

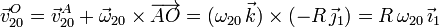
$\vec{v}_{20}^O = \vec{v}_{20}^A+\vec{\omega}_{20}\times\overrightarrow{AO}=(\omega_{20}\,\vec{k})\times(-R\,\vec{\jmath}_1)=R\,\omega_{20}\,\vec{\imath}_1$

Aplicamos la composición de movimientos de velocidades en $A$ para obtener el valor de $ω 01$

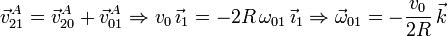
$\vec{v}_{21}^A=\vec{v}_{20}^A+\vec{v}_{01}^A\Rightarrow v_0\,\vec{\imath}_1=-2R\,\omega_{01}\,\vec{\imath}_1\Rightarrow \vec{\omega}_{01}=-\dfrac{v_0}{2R}\,\vec{k}$

Y ahora la composición de velocidades angulares para obtener $ω 20$

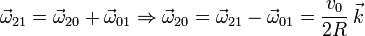
$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}\Rightarrow\vec{\omega}_{20}=\vec{\omega}_{21}-\vec{\omega}_{01}=\dfrac{v_0}{2R}\,\vec{k}$

Y ahora ya podemos calcular las reducciones pedidas

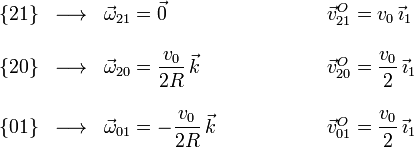
$\begin{array}{lclcl} \{21\}&\longrightarrow&\vec{\omega}_{21}=\vec{0}&\qquad\qquad&\vec{v}_{21}^O=v_0\,\vec{\imath}_1\\ &&&&\\ \{20\}&\longrightarrow&\vec{\omega}_{20}=\dfrac{v_0}{2R}\,\vec{k}&\qquad\qquad&\vec{v}_{20}^O=\dfrac{v_0}{2}\,\vec{\imath}_1\\ &&&&\\ \{01\}&\longrightarrow&\vec{\omega}_{01}=-\dfrac{v_0}{2R}\,\vec{k}&\qquad\qquad&\vec{v}_{01}^O=\dfrac{v_0}{2}\,\vec{\imath}_1 \end{array}$

2.4 Aceleración a^A₂₀

Debido a que el movimiento {21} de la barra tiene velocidad constante, tenemos

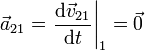
$\vec{a}_{21} = \left.\dfrac{\mathrm{d}\vec{v}_{21}}{\mathrm{d}t}\right|_1=\vec{0}$

No particularizamos en un punto pues al ser una traslación es igual para todos. Por otro lado, el movimiento {01} del punto $O$ del sólido "0" también es de velocidad constante. Y también es constante en el tiempo $\vec{\omega}_{01}$ . Por tanto

$\vec{\alpha}_{01}=\vec{0}\qquad\qquad\vec{a}_{01}^O=\vec{0}$

Usando la ley de composición de aceleraciones

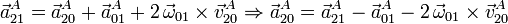
$\vec{a}_{21}^A = \vec{a}_{20}^A+\vec{a}_{01}^A+2\,\vec{\omega}_{01}\times\vec{v}_{20}^A\Rightarrow \vec{a}_{20}^A = \vec{a}_{21}^A-\vec{a}_{01}^A-2\,\vec{\omega}_{01}\times\vec{v}_{20}^A$

Calculamos 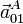$\vec{a}_{01}^A$ usando la ecuación del campo de aceleraciones del movimiento {01}

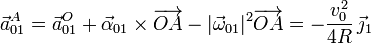
$\vec{a}_{01}^A = \vec{a}_{01}^O+\vec{\alpha}_{01}\times\overrightarrow{OA}-|\vec{\omega}_{01}|^2\overrightarrow{OA}=-\dfrac{v_0^2}{4R}\,\vec{\jmath}_1$

El resultado final es

$\vec{a}_{20}^A=\dfrac{v_0^2}{4R}\,\vec{\jmath}_1$

@@ Línea 69: / Línea 69: @@
 </math></center>
-===Aceleración a<sub>20</sub><sup>A</sup> ===
+===Aceleración a<sup>A</sup><sub>20</sub> ===
 Debido a que el movimiento {21} de la barra tiene velocidad
 constante, tenemos
@@ Línea 97: / Línea 97: @@
    \vec{a}_{20}^A=\dfrac{v_0^2}{4R}\,\vec{\jmath}_1
 </math></center>
+[[Categoría: Problemas de movimiento plano]]

Barra horizontal sobre un disco (G.I.A.)

De Laplace

última version al 17:20 10 ene 2014

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {21}

2.2 Movimiento {01}

2.3 Movimiento {20}

2.4 Aceleración a^A₂₀

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra horizontal sobre un disco (G.I.A.)

De Laplace

última version al 17:20 10 ene 2014

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {21}

2.2 Movimiento {01}

2.3 Movimiento {20}

2.4 Aceleración aA20

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.4 Aceleración a^A₂₀