Entrar Página Discusión Historial Go to the site toolbox

Masa suspendida de dos muelles

De Laplace

(Diferencias entre revisiones)
(→Equilibrio en paralelo)
Línea 11: Línea 11:
[[Archivo:resortes-paralelo.png|right]]
[[Archivo:resortes-paralelo.png|right]]
-
Consideremos en primer lugar el caso de dos resortes de constantes <math>k_1</math> y <math>k_2</math> y longitudes en reposo <math>l_{10}</math> y <math>l_{20}</math>, que cuelgan del techo y una masa <math>m</math> suspendida de ambos muelles simultáneamente. ¿Cuál es la posición de equilibrio y con qué frecuencia oscila la masa?
+
Para analizar el problema, consideramos un sistema de ejes en el que la dirección vertical y hacia abajo es el eje OX. Puesto que todos los desplazamientos y fuerzas van a ir en esta dirección, podemos usar cantidades escalares. El signo positivo indicará una fuerza o desplazamiento hacia abajo y el signo negativo uno hacia arriba.
 +
 
 +
Tenemos en primer lugar el caso de dos resortes de constantes <math>k_1= 900\,\mathrm{N}/\mathrm{m}</math> y <math>k_2=1600\,\mathrm{N}/\mathrm{m}</math> y longitudes en reposo <math>l_{10}=l_{20}=10\,\mathrm{cm}</math>, que cuelgan del techo y una masa <math>m=1\,\mathrm{kg}</math> suspendida de ambos muelles simultáneamente. ¿Dónde está la posición de equilibrio?
Sea <math>l</math> la longitud que adquieren ambos resortes (que será necesariamente la misma para los dos).  
Sea <math>l</math> la longitud que adquieren ambos resortes (que será necesariamente la misma para los dos).  
Línea 19: Línea 21:
La ecuación de movimiento para la masa es
La ecuación de movimiento para la masa es
-
<center><math>a = \frac{F}{m}=\frac{1}{m}\left(F_1+F_2+mg\right)</math></center>
+
<center><math>ma = F= F_1+F_2+mg</math></center>
siendo <math>F_1</math> y <math>F_2</math> las fuerzas producidas por cada una de los resortes
siendo <math>F_1</math> y <math>F_2</math> las fuerzas producidas por cada una de los resortes
Línea 29: Línea 31:
<center><math>-k_1(l-l_{10}) - k_2(l-l_{20}) + mg = 0\qquad\Rightarrow\qquad l_\mathrm{eq} = \frac{k_1l_{10}+k_2l_{20}+mg}{k_1+k_2}</math></center>
<center><math>-k_1(l-l_{10}) - k_2(l-l_{20}) + mg = 0\qquad\Rightarrow\qquad l_\mathrm{eq} = \frac{k_1l_{10}+k_2l_{20}+mg}{k_1+k_2}</math></center>
-
Podemos comprobar que en este resultado si <math>k_1\to\infty</math> (el primer muelle se hace infinitamente rígido)
+
Numéricamente
-
<center><math>\lim_{k_1\to\infty}l_\mathrm{eq} = l_{10}</math></center>
+
<center><math>l_\mathrm{eq}=\frac{900\times 0.1+1600\times 0.1+1\times 9.81}{900+1600}\,\mathrm{m}=0.104\,\mathrm{m}=10.4\,\mathrm{cm}</math></center>
-
esto es, este resorte no se estira en absoluto. Igualmente si hacemos <math>k_2\to\infty</math>, es el segundo muelle el que no se estira.
+
Vemos que la deformación es pequeña por ser los dos muelles mu rígidos.
 +
==Oscilación en paralelo==
Definiendo la posición respecto a la de equilibrio
Definiendo la posición respecto a la de equilibrio
Línea 62: Línea 65:
En general, siempre que tengamos dos, tres,... resortes atados a distintos anclajes fijos (que pueden estar en diferentes puntos del espacio) y todos a la misma masa <math>m</math>, la constante equivalente de la asociación es igual a la suma de las constantes individuales.
En general, siempre que tengamos dos, tres,... resortes atados a distintos anclajes fijos (que pueden estar en diferentes puntos del espacio) y todos a la misma masa <math>m</math>, la constante equivalente de la asociación es igual a la suma de las constantes individuales.
-
 
-
==Oscilación en paralelo==
 
==Equilibrio en serie==
==Equilibrio en serie==
==Oscilación en serie==
==Oscilación en serie==
[[Categoría:Problemas de dinámica de la partícula (GIE)]]
[[Categoría:Problemas de dinámica de la partícula (GIE)]]

Revisión de 17:38 23 dic 2013

Contenido

1 Enunciado

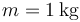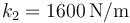Se dispone de una masa m=1\,\mathrm{kg} y de resortes de longitud natural 10 cm y constantes k_1= 900\,\mathrm{N}/\mathrm{m} y k_2=1600\,\mathrm{N}/\mathrm{m}.

  1. Suponga que se cuelga la masa del techo colocando en paralelo los dos resortes. En el equilibrio, ¿cuál es la distancia de la masa al techo?
  2. Para este caso, si la masa está en la posición de equilibrio y se le comunica una velocidad de 10 cm/s hacia arriba, ¿cuál es la amplitud de las oscilaciones resultantes? ¿Y su frecuencia?
  3. Suponga ahora que los resortes se conectan en serie, uno a continuación del otro y se suspenden del techo, con la masa en el extremo inferior. ¿Cuánto se estira cada resorte?
  4. Si para este segundo caso se le comunica a la masa en el equilibrio una velocidad de 10 cm/s hacia abajo, ¿cuál es la amplitud y la frecuencia de las oscilaciones?

2 Equilibrio en paralelo

Para analizar el problema, consideramos un sistema de ejes en el que la dirección vertical y hacia abajo es el eje OX. Puesto que todos los desplazamientos y fuerzas van a ir en esta dirección, podemos usar cantidades escalares. El signo positivo indicará una fuerza o desplazamiento hacia abajo y el signo negativo uno hacia arriba.

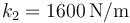Tenemos en primer lugar el caso de dos resortes de constantes k_1= 900\,\mathrm{N}/\mathrm{m} y k_2=1600\,\mathrm{N}/\mathrm{m} y longitudes en reposo 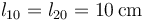l_{10}=l_{20}=10\,\mathrm{cm}, que cuelgan del techo y una masa 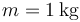m=1\,\mathrm{kg} suspendida de ambos muelles simultáneamente. ¿Dónde está la posición de equilibrio?

Sea l la longitud que adquieren ambos resortes (que será necesariamente la misma para los dos).

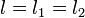
l = l_1 = l_2\,

La ecuación de movimiento para la masa es

ma = F = F1 + F2 + mg

siendo F1 y F2 las fuerzas producidas por cada una de los resortes

F_1 = -k_1(l-l_{10})\qquad F_2 = -k_2(l-l_{20})

La posición de equilibrio nos la da el que la fuerza sea cero

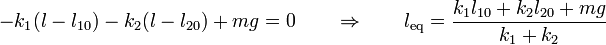
-k_1(l-l_{10}) - k_2(l-l_{20}) + mg = 0\qquad\Rightarrow\qquad l_\mathrm{eq} = \frac{k_1l_{10}+k_2l_{20}+mg}{k_1+k_2}

Numéricamente

l_\mathrm{eq}=\frac{900\times 0.1+1600\times 0.1+1\times 9.81}{900+1600}\,\mathrm{m}=0.104\,\mathrm{m}=10.4\,\mathrm{cm}

Vemos que la deformación es pequeña por ser los dos muelles mu rígidos.

3 Oscilación en paralelo

Definiendo la posición respecto a la de equilibrio

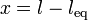
x = l-l_\mathrm{eq}\,

la ecuación de movimiento se convierte en

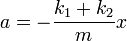
a = -\frac{k_1+k_2}{m}x

que nos dice que el muelle oscila en torno a su posición de equilibrio con una constante equivalente a la asociación que es la suma de las constantes individuales

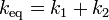
k_\mathrm{eq}=k_1+k_2\,

de forma que la frecuencia de oscilación vale

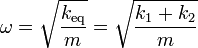
\omega = \sqrt{\frac{k_\mathrm{eq}}{m}}=\sqrt{\frac{k_1+k_2}{m}}

En particular, si las dos constantes son iguales, esto nos da una constante equivalente que es el doble de cada una de ellas.

Cuando tenemos dos muelles suspendidos en paralelo, la elongación de ambos, respecto a la posición de equilibrio, es necesariamente la misma, mientras que la fuerza es la suma de la que produce cada resorte

x = x_1 = x_2\,\qquad\qquad F= F_1+F_2

De aquí la relación entre las constantes es inmediata

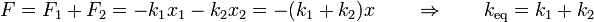
F = F_1 + F_2 = -k_1 x_1 - k_2 x_2 = -(k_1+k_2)x\qquad \Rightarrow\qquad k_\mathrm{eq}=k_1+k_2

En general, siempre que tengamos dos, tres,... resortes atados a distintos anclajes fijos (que pueden estar en diferentes puntos del espacio) y todos a la misma masa m, la constante equivalente de la asociación es igual a la suma de las constantes individuales.

4 Equilibrio en serie

5 Oscilación en serie

Obtenido de "http://tesla.us.es/wiki/index.php/Masa_suspendida_de_dos_muelles"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace