Máquina de Atwood simple
De Laplace
(→Enunciado) |
|||
| Línea 53: | Línea 53: | ||
Vemos que no es simplemente igual al peso de las dos masas, sino que influye el que éstas estén aceleradas. Esta fuerza debe ser contrarrestada por el anclaje de la polea, que debe ejercer una fuerza igual y de sentido contrario <math>\vec{F}_\mathrm{ext}=-\vec{F}</math>. | Vemos que no es simplemente igual al peso de las dos masas, sino que influye el que éstas estén aceleradas. Esta fuerza debe ser contrarrestada por el anclaje de la polea, que debe ejercer una fuerza igual y de sentido contrario <math>\vec{F}_\mathrm{ext}=-\vec{F}</math>. | ||
| - | [[Categoría:Problemas de | + | [[Categoría:Problemas de dinámica de la partícula (GIE)]] |
Revisión de 22:09 14 nov 2013
1 Enunciado
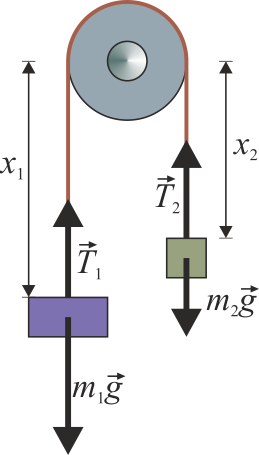
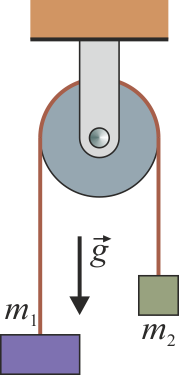
Una máquina de Atwood es un dispositivo simple compuesto por una polea por la que pasa una cuerda, de cuyos extremos penden dos masas m1 y m2. En el caso ideal se supone que la cuerda es inextensible y sin masa, y que la polea tampoco tiene masa ni fricción.
Para este caso ideal, calcule la aceleración de cada masa, la tensión de la cuerda y la fuerza que ejerce el gancho que sujeta la polea.
2 Solución
Una de las aplicaciones de las tensiones de hilos es el de la máquina de Atwood, formada por dos masas m1 y m2 unidas por un hilo ideal que pasa por una polea también ideal. Cuando se liberan estas masas, la más pesada tira de las más ligera y comienzan a moverse aceleradamente. La cuestión es calcular con qué aceleración lo hacen.
Para la masa m1, las fuerzas que actúan sobre ella son su peso y la tensión del hilo, de forma que
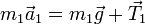
Puesto que todas las fuerzas son verticales, podemos usar cantidades escalares
y queda

Haciendo los mismo para la segunda masa
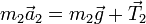
Por ser la cuerda inextensible, la aceleración con la que se estira por un lado debe ser exactamente igual que con la que se recoge por otro.
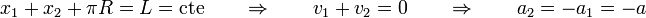
Por otro lado, como el módulo de la tensión del hilo es el mismo a lo largo de todos sus puntos

lo que nos da la ecuación escalar
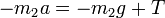
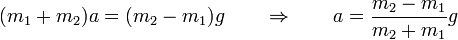
y si queremos la tensión del hilo

La fuerza sobre la polea la da en que está sometida a la tensión que tira de ella por sus dos extremos
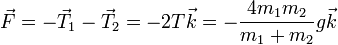
Vemos que no es simplemente igual al peso de las dos masas, sino que influye el que éstas estén aceleradas. Esta fuerza debe ser contrarrestada por el anclaje de la polea, que debe ejercer una fuerza igual y de sentido contrario 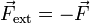 .
.