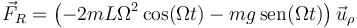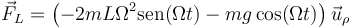Fuerza en anilla ensartada en varillas

De Laplace

(Diferencias entre revisiones)

Revisión de 00:11 14 nov 2013

1 Enunciado

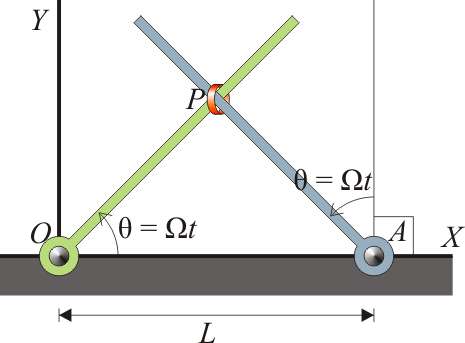
Para el sistema de la anilla ensartada en dos varillas, calcule la fuerza que cada una de las barras ejerce cada instante sobre la anilla, suponiendo ´esta de masa m, (a) despreciando el peso, (b) considerando el peso en la dirección de OY negativo. Tenga en cuenta que cada barra solo puede ejercer fuerza perpendicularmente a sí misma, no a lo largo de ella.

2 Sin considerar el peso

Conocemos el movimiento de la anilla; se ve en este problema y en este otro: describe un movimiento circular uniforme en torno al punto medio de los dos anclajes, siendo su velocidad angular $2Ω$ y el radio de giro $L / 2$ . La ecuación horaria del movimiento es, respecto al anclaje de la izquierda,

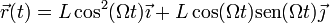
$\vec{r}(t) = L\cos^2(\Omega t)\vec{\imath}+L\cos(\Omega t)\mathrm{sen}(\Omega t)\vec{\jmath}$

o, expresada en coordenadas polares respecto a este mismo punto

$\rho = L\cos(\Omega t)\qquad\qquad \varphi = \Omega t$

La fuerza neta que actúa sobre la anilla nos la da la segunda ley de Newton

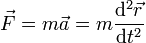
$\vec{F}=m\vec{a}=m\frac{\mathrm{d}^2\vec{r}}{\mathrm{d}t^2}$

que en coordenadas polares queda

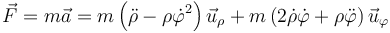
$\vec{F}=m\vec{a}=m\left(\ddot{\rho}-\rho\dot{\varphi}^2\right)\vec{u}_\rho + m\left(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi}\right)\vec{u}_\varphi$

Si no consideramos el peso, las fuerzas que actúan sobre la anilla se deben exclusivamente a las dos varillas

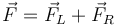
$\vec{F}=\vec{F}_L+\vec{F}_R$

La varilla de la derecha ejerce sobre la anilla una fuerza $\vec{F}_R$ . Esta fuerza es siempre perpendicular a la propia varilla (ya que ésta no puede impedir que la anilla) se mueva a lo largo de ella. Pero la perpendicular a la varilla de la derecha es justamente la dirección de la varilla de la izquierda, que a su vez es la dirección radial desde O. Por tanto

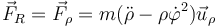
$\vec{F}_R = \vec{F}_\rho = m(\ddot{\rho}-\rho\dot{\varphi}^2)\vec{u}_\rho$

Calculamos los términos que aparecen en esta expresión

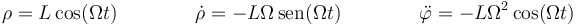
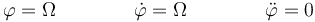
$\rho = L\cos(\Omega t)\qquad\qquad \dot{\rho}=-L\Omega\,\mathrm{sen}(\Omega t)\qquad\qquad \ddot{\varphi}=-L\Omega^2\cos(\Omega t)$ $\varphi = \Omega \qquad\qquad\dot{\varphi}=\Omega\qquad\qquad \ddot{\varphi}=0$

y por tanto

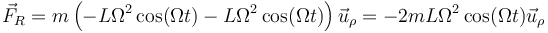
$\vec{F}_R = m\left(-L\Omega^2\cos(\Omega t)-L\Omega^2\cos(\Omega t)\right)\vec{u}_\rho=-2mL\Omega^2\cos(\Omega t)\vec{u}_\rho$

Asimismo, la fuerza ejercida por la varilla de la izquierda 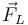$\vec{F}_L$ va en la dirección perpendicular a ella misma. Por tanto 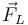$\vec{F}_L$ va en la dirección de 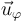$\vec{u}_\varphi$ y es igual a

$\vec{F}_L = m(2\dot{\rho}\dot{\varphi}+\rho\ddot{\varphi})\vec{u}_\varphi = -2mL\Omega^2\mathrm{sen}(\Omega t)\vec{u}_\varphi$

3 Incluyendo el peso

Cuando se considera el peso, el cálculo es similar, ya que podemos aplicar el principio de superposición. Incluyendo el peso, la ecuación de movimiento queda

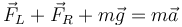
$\vec{F}_L+\vec{F}_R + m\vec{g} = m\vec{a}$

o, equivalentemente,

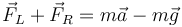
$\vec{F}_L+\vec{F}_R = m\vec{a} - m\vec{g}$

Incluso si consideramos el peso, la aceleración es la misma que en el apartado anterior, ya que el movimiento de la anilla está gobernado por las barras. la anilla tiene 0 grados de libertad.

Como en el apartado anterior

$\vec{F}_R=F_\rho\vec{u}_\rho\qquad\qquad \vec{F}_R=F_\varphi\vec{u}_\varphi$

Lo único que nos resta hacer es descomponer el peso en sus componentes polares. Esto se consigue empleando la relación entre bases:

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \vec{\jmath}=\mathrm{sen}(\varphi)\vec{u}_\rho}+\cos(\varphi)\vec{u}_\varphi

y por tanto

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): m\vec{g}=-mg\vec{\jmath} = -mg\,\mathrm{sen}(\varphi)\vec{u}_\rho}-mg\cos(\varphi)\vec{u}_\varphi

Sumando esto a los resultados que ya teníamos nos queda

$\vec{F}_R =\left( -2mL\Omega^2\cos(\Omega t)-mg\,\mathrm{sen}(\Omega t)\right)\vec{u}_\rho$ $\vec{F}_L =\left( -2mL\Omega^2\mathrm{sen}(\Omega t)-mg\,\mathrm{cos}(\Omega t)\right)\vec{u}_\rho$

@@ Línea 48: / Línea 48: @@
 Cuando se considera el peso, el cálculo es similar, ya que podemos aplicar el principio de superposición. Incluyendo el peso, la ecuación de movimiento queda
-<center><math>\vec{F}_1+\vec{F}_2 + m\vec{g} = m\vec{a}</math></center>
+<center><math>\vec{F}_L+\vec{F}_R + m\vec{g} = m\vec{a}</math></center>
 o, equivalentemente,
-<center><math>\vec{F}_1+\vec{F}_2 = m\vec{a} - m\vec{g}</math></center>
+<center><math>\vec{F}_L+\vec{F}_R = m\vec{a} - m\vec{g}</math></center>
-Incluso si consideramos el peso, la aceleración es la misma que en el apartado anterior, ya que el movimiento de la anilla está gobernado por las barras. la anilla tiene 0 grados de libertad. Por ello podemos hallar las fuerzas debida a las barras como suma de 2
+Incluso si consideramos el peso, la aceleración es la misma que en el apartado anterior, ya que el movimiento de la anilla está gobernado por las barras. la anilla tiene 0 grados de libertad.
-<center><math>\vec{F}_1 = \vec{F}_{1a}+\vec{F}_{1g}\qquad\qquad \vec{F}_2 = \vec{F}_{2a}+\vec{F}_{2g}</math></center>
+Como en el apartado anterior
-tales que
+<center><math>\vec{F}_R=F_\rho\vec{u}_\rho\qquad\qquad \vec{F}_R=F_\varphi\vec{u}_\varphi</math></center>
-<center><math>\vec{F}_{1a}+\vec{F}_{2a}=m\vec{a}\qquad \qquad \vec{F}_{1g}+\vec{F}_{2g}=-m\vec{g}</math></center>
+Lo único que nos resta hacer es descomponer el peso en sus componentes polares. Esto se consigue empleando la relación entre bases:
-Las dos primeras son las mismas que se calcularon en la sección anterior. Solo queda descomponer el peso (cambiado de signo) en suma de dos fuerzas perpendiculares a las barras.
+<center><math>\vec{\jmath}=\mathrm{sen}(\varphi)\vec{u}_\rho}+\cos(\varphi)\vec{u}_\varphi</math></center>
-[[Archivo:Fuerza-dos-varillas-02.png|right]]
+y por tanto
-El peso forma un ángulo <math>\theta=\Omega t</math> con la barra 2 y su complementario con la barra 1. Por ello, se cumple
+<center><math>m\vec{g}=-mg\vec{\jmath} = -mg\,\mathrm{sen}(\varphi)\vec{u}_\rho}-mg\cos(\varphi)\vec{u}_\varphi</math></center>
-<center><math>|\vec{F}_{1g}| =mg\cos(\Omega t)\qquad |\vec{F}_{2g}| =mg\,\mathrm{sen}(\Omega t)</math></center>
+Sumando esto a los resultados que ya teníamos nos queda
-y, en forma vectorial
+<center><math>\vec{F}_R =\left( -2mL\Omega^2\cos(\Omega t)-mg\,\mathrm{sen}(\Omega t)\right)\vec{u}_\rho</math></center>
-<center><math>\vec{F}_{1g}= mg\cos(\Omega t)\vec{u}_2\qquad\qquad  \vec{F}_{2g}= mg\,\mathrm{sen}(\Omega t)\vec{u}_1</math></center>
+<center><math>\vec{F}_L =\left( -2mL\Omega^2\mathrm{sen}(\Omega t)-mg\,\mathrm{cos}(\Omega t)\right)\vec{u}_\rho</math></center>
-En la base cartesiana
-<center><math>\vec{F}_{1g}=mg\left(-\,\mathrm{sen}(\Omega t)\cos(\Omega t)\vec{\imath}+\cos^2(\Omega t)\vec{\jmath}\right)
-</math></center>
-y
-<center><math>
-\vec{F}_{2g}=mg\left(\,\mathrm{sen}(\Omega t)\cos(\Omega t)\vec{\imath}+\mathrm{sen}^2(\Omega t)\vec{\jmath}\right)</math></center>
-La suma de estas dos da una fuerza constante en la dirección vertical, como corresponde al peso.
-Sumando cada una con al correspondiente del apartado anterior obtenemos la fuerza ejercida por cada una de las barras.
-<center><math>\vec{F}_{1}= \left(-2m\Omega^2L\,\mathrm{sen}(\Omega t)+mg\cos(\Omega t)\right)\vec{u}_2</math></center>
-y
-<center><math>\vec{F}_{2}= \left(-2m\Omega^2L\,\mathrm{cos}(\Omega t)+mg\,\mathrm{sen}(\Omega t)\right)\vec{u}_1</math></center>
 [[Categoría:Problemas de dinámica de la partícula (GIE)]]

Fuerza en anilla ensartada en varillas

De Laplace

Revisión de 00:11 14 nov 2013

1 Enunciado

2 Sin considerar el peso

3 Incluyendo el peso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES