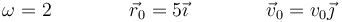Oscilador armónico tridimensional
De Laplace
(Diferencias entre revisiones)
(→Solución general) |
|||
| Línea 20: | Línea 20: | ||
<center><math>\vec{r}(t) = \vec{r}_0\cos(\omega t)+\frac{\vec{v}_0}\mathrm{sen}(\omega t)</math></center> | <center><math>\vec{r}(t) = \vec{r}_0\cos(\omega t)+\frac{\vec{v}_0}\mathrm{sen}(\omega t)</math></center> | ||
| + | |||
| + | siendo <math>\vec{r}_0</math> la posición inicial y <math>\vec{v}_0</math> la velocidad inicial de la partícula. | ||
| + | |||
| + | En este problema tenemos para todos los casos, empleando las unidades fundamentales del SI, | ||
| + | |||
| + | <center><math>\omega = 2\qquad\qquad\vec{r}_0=5\vec{\imath}\qquad\qquad\vec{v}_0=v_0\vec{\jmath}</math></center> | ||
| + | |||
==Caso v<sub>0</sub> = 0 m/s== | ==Caso v<sub>0</sub> = 0 m/s== | ||
==Caso v<sub>0</sub> = 10 m/s== | ==Caso v<sub>0</sub> = 10 m/s== | ||
Revisión de 15:27 10 nov 2013
Contenido |
1 Enunciado
Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico
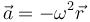
con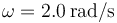 
. Su posición inicial es 
.
- Para el caso
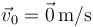. ¿Qué tipo de movimiento describe la partícula?
- Para el caso
, ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
- Suponga ahora que
, ¿cómo es ahora la trayectoria de la partícula?
- Para los tres casos anteriores, determine
- la rapidez,
- las componentes intrínsecas de la aceleración,
- los vectores tangente y normal,
- el radio de curvatura y el centro de curvatura.
- para los instantes
, 
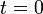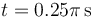y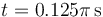 
.
2 Solución general
La solución general de la ecuación del oscilador armónico en 3D es de la forma
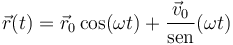
siendo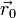 
la posición inicial y 
la velocidad inicial de la partícula.
En este problema tenemos para todos los casos, empleando las unidades fundamentales del SI,
