Movimiento circular en 3D

De Laplace

(Diferencias entre revisiones)

Revisión de 18:40 7 nov 2013

Contenido

1 Enunciado
2 Trayectoria
- 2.1 Identificación geométrica
- 2.2 Procedimiento cinemático

1 Enunciado

Una partícula se mueve según las ecuaciones horarias

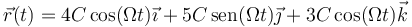
$\vec{r}(t)=4C\cos(\Omega t)\vec{\imath}+ 5C\,\mathrm{sen}(\Omega t)\vec{\jmath}+3C\cos(\Omega t)\vec{k}$

con C y Ω constantes.

¿Qué trayectoria sigue la partícula?
¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
¿Qué tipo de movimiento describe la partícula?

2 Trayectoria

Podemos identificar la trayectoria a partir de razonamientos puramente geométricos o empleando procedimientos cinemáticos.

2.1 Identificación geométrica

Si separamos las tres componentes del movimiento

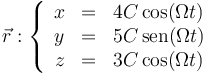
$\vec{r}:\left\{\begin{array}{rcl} x & = &4C\cos(\Omega t) \\ y & = & 5C\,\mathrm{sen}(\Omega t)\\ z & = & 3C\cos(\Omega t)\end{array}\right.$

De aquí es evidente que

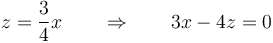
$z = \frac{3}{4}x\qquad\Rightarrow\qquad 3x-4z =0$

Esta es la ecuación de un plano. También la podemos escribir en forma vectorial como

$\vec{B}\cdot\vec{r}=0\qquad\qquad \vec{B}=\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{\jmath}$

El vector $\vec{B}$ es un vector constante ortogonal al plano de movimiento.

Además tenemos que se cumple

$x^2 + z^2 = 25C^2\cos^2(\Omega t)\qquad\qquad y^2 = 25C^2\mathrm{sen}^2(\Omega t)$

y sumando estas dos

$x^2 + y^2 + z^2 = 25C^2\,$

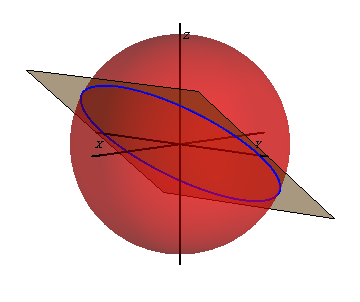
que es la ecuación de una esfera de radio $R = 5 C$ .

la trayectoria es entonces la intersección de un plano y una esfera. Esa intersección es siempre una circunferencia. Por tanto el movimiento es circular.

2.2 Procedimiento cinemático

El método anterior es muy simple para determinar que el movimiento es plano, pero no siempre se encuentra a la primera qué combinación lineal de las variables nos da la ecuación del plano, si este existe.

Por ello, existen procedimiento sistemáticos para determinar esta situación.

Uno es el siguiente: hay que hallar la velocidad, la aceleración y la derivada de ésta respecto al tiempo. El movimiento es plano si y solo si se cumple la condición

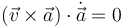
$(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}=0$

En nuestro caso tenemos

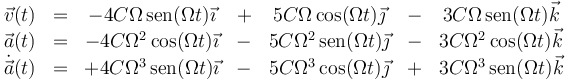
$\begin{array}{ccccccc} \vec{v}(t) & = & -4C\Omega\,\mathrm{sen}(\Omega t)\vec{\imath}& + & 5C\Omega\,\mathrm{cos}(\Omega t)\vec{\jmath}& - & 3C\Omega\,\mathrm{sen}(\Omega t)\vec{k}\\ \vec{a}(t)& = & -4C\Omega^2\,\mathrm{cos}(\Omega t)\vec{\imath}& - & 5C\Omega^2\,\mathrm{sen}(\Omega t)\vec{\jmath}& - & 3C\Omega^2\,\mathrm{cos}(\Omega t)\vec{k}\\ \dot{\vec{a}}(t) & = & +4C\Omega^3\,\mathrm{sen}(\Omega t)\vec{\imath}& - &5C\Omega^3\,\mathrm{cos}(\Omega t)\vec{\jmath}& + & 3C\Omega^3\,\mathrm{sen}(\Omega t)\vec{k}\end{array}$

El producto vectorial de la velocidad y la aceleración lo da el el determinante

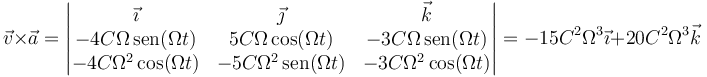
$\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -4C\Omega\,\mathrm{sen}(\Omega t) & 5C\Omega\,\mathrm{cos}(\Omega t)& - 3C\Omega\,\mathrm{sen}(\Omega t)\\ -4C\Omega^2\,\mathrm{cos}(\Omega t)& -5C\Omega^2\,\mathrm{sen}(\Omega t)& -3C\Omega^2\,\mathrm{cos}(\Omega t)\end{matrix}\right|=-15C^2\Omega^3\vec{\imath}+20C^2\Omega^3\vec{k}$

Siendo el producto mixto de los tres vectores

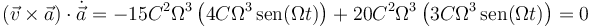
$(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}= -15C^2\Omega^3\left(4C\Omega^3\,\mathrm{sen}(\Omega t)\right)+20C^2\Omega^3\left(3C\Omega^3\,\mathrm{sen}(\Omega t)\right)=0$

Con eso ya tenemos que la trayectoria es plana. Para ver que además es circular vamos a calcular el radio de curvatura, según la fórmula

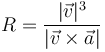
$R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}$

La rapidez del movimiento vale

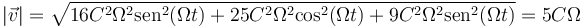
$|\vec{v}|=\sqrt{16C^2\Omega^2\mathrm{sen}^2(\Omega t)+25C^2\Omega^2\mathrm{cos}^2(\Omega t)+9C^2\Omega^2\mathrm{sen}^2(\Omega t)}=5C\Omega$

Esta cantidad es constante por lo que ya sabemos además que el movimiento es uniforme.

Hallamos ahora el radio de curvatura

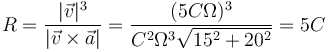
$R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}=\frac{(5C\Omega)^3}{C^2\Omega^3\sqrt{15^2+20^2}}=5C$

El radio de curvatura es constante.

Si el movimiento es plano y el radio de curvatura es constante, se trata de un movimiento circular.

@@ Línea 67: / Línea 67: @@
 <center><math>(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}=
--15\left(4C\Omega^3\,\mathrm{sen}(\Omega t)\right)+20\left(3C\Omega^3\,\mathrm{sen}(\Omega t)\right)=0</math></center>
+-15C^2\Omega^3\left(4C\Omega^3\,\mathrm{sen}(\Omega t)\right)+20C^2\Omega^3\left(3C\Omega^3\,\mathrm{sen}(\Omega t)\right)=0</math></center>
-Podemos ver que este determinante se anula sin necesidad de desarrollarlo porque la tercera fila es igual a la primera multiplicada por <math>-\Omega^2</math>, o la tercera columna igual a la primera multiplicada por 3/4.
 Con eso ya tenemos que la trayectoria es plana. Para ver que además es circular vamos a calcular el radio de curvatura, según la fórmula
@@ Línea 81: / Línea 79: @@
 Esta cantidad es constante por lo que ya sabemos además que el movimiento es uniforme.
+Hallamos ahora el radio de curvatura
+<center><math>R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}=\frac{(5C\Omega)^3}{C^2\Omega^3\sqrt{15^2+20^2}}=5C</math></center>
+El radio de curvatura es constante.
+Si el movimiento es plano y el radio de curvatura es constante, se trata de un movimiento circular.
 [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]]

Movimiento circular en 3D

De Laplace

Revisión de 18:40 7 nov 2013

Contenido

1 Enunciado

2 Trayectoria

2.1 Identificación geométrica

2.2 Procedimiento cinemático

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES