Movimiento circular en 3D
De Laplace
(Diferencias entre revisiones)
(→Identificación geométrica) |
(→Trayectoria) |
||
| Línea 16: | Línea 16: | ||
Si separamos las tres componentes del movimiento | Si separamos las tres componentes del movimiento | ||
| - | <center><math>\vec{r}:\left\{\begin{array}{rcl} x & = & | + | <center><math>\vec{r}:\left\{\begin{array}{rcl} x & = &4C\cos(\Omega t) \\ y & = & 5C\,\mathrm{sen}(\Omega t)\\ z & = & 3C\cos(\Omega t)\end{array}\right.</math></center> |
| + | |||
| + | De aquí es evidente que | ||
| + | |||
| + | <center><math>z = \frac{3}{4}x\qquad\Rightarrow\qquad 3x-4z =0</math></center> | ||
| + | |||
| + | Esta es la ecuación de un plano. También la podemos escribir en forma vectorial como | ||
| + | |||
| + | <center><math>\vec{B}\cdot\vec{r}=0\qquad\qquad \vec{B}=\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{\jmath}</math></center> | ||
| + | |||
| + | El vector <math>\vec{B}</math> es un vector constante ortogonal al plano de movimiento. | ||
| + | |||
| + | Además tenemos que se cumple | ||
| + | |||
| + | <center><math>x^2 + z^2 = 25C^2\cos^2(\Omega t)\qquad\qquad y^2 = 25C^2\mathrm{sen}^2(\Omega t)</math></center> | ||
| + | |||
| + | y sumando estas dos | ||
| + | |||
| + | <center><math>x^2 + y^2 + z^2 = 25C^2\,</math></center> | ||
| + | |||
| + | que es la ecuación de una esfera de radio <math>R=5C</math>. | ||
| + | |||
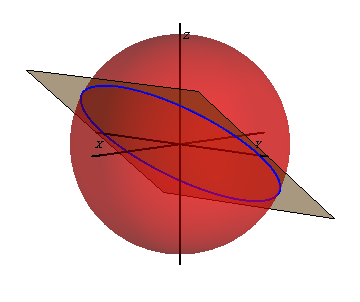
| + | la trayectoria es entonces la intersección de un plano y una esfera. Esa intersección es siempre una circunferencia. Por tanto el movimiento es circular. | ||
| + | |||
| + | <center>[[Archivo:corte-plano-esfea.png]]</center> | ||
[[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | ||
Revisión de 18:30 7 nov 2013
1 Enunciado
Una partícula se mueve según las ecuaciones horarias
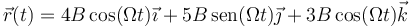
con B y Ω constantes.
- ¿Qué trayectoria sigue la partícula?
- ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
- ¿Qué tipo de movimiento describe la partícula?
2 Trayectoria
Podemos identificar la trayectoria a partir de razonamientos puramente geométricos o empleando procedimientos cinemáticos.
2.1 Identificación geométrica
Si separamos las tres componentes del movimiento
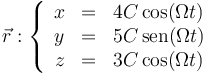
De aquí es evidente que
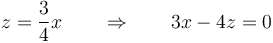
Esta es la ecuación de un plano. También la podemos escribir en forma vectorial como

El vector  es un vector constante ortogonal al plano de movimiento.
es un vector constante ortogonal al plano de movimiento.
Además tenemos que se cumple

y sumando estas dos

que es la ecuación de una esfera de radio R = 5C.
la trayectoria es entonces la intersección de un plano y una esfera. Esa intersección es siempre una circunferencia. Por tanto el movimiento es circular.