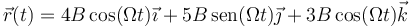|
|
| (36 ediciones intermedias no se muestran.) |
| Línea 2: |
Línea 2: |
| | Una partícula se mueve según las ecuaciones horarias | | Una partícula se mueve según las ecuaciones horarias |
| | | | |
| - | <center><math>\vec{r}(t)=4A\cos(\Omega t)\vec{\imath}+ 5A\,\mathrm{sen}(\Omega t)\vec{\jmath}+3A\cos(\Omega t)\vec{k}</math></center> | + | <center><math>\vec{r}(t)=4B\cos(\Omega t)\vec{\imath}+ 5B\,\mathrm{sen}(\Omega t)\vec{\jmath}+3B\cos(\Omega t)\vec{k}</math></center> |
| | | | |
| - | con A y Ω constantes. | + | con B y Ω constantes. |
| | | | |
| | # ¿Qué trayectoria sigue la partícula? | | # ¿Qué trayectoria sigue la partícula? |
| | # ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω? | | # ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω? |
| - | # Justifique que este movimiento es circular y uniforme | + | # ¿Qué tipo de movimiento describe la partícula? |
| - | # Determine la posición del centro del movimiento circular
| + | |
| - | # Calcule la velocidad angular de este movimiento circular
| + | |
| | | | |
| | ==Trayectoria== | | ==Trayectoria== |
| Línea 18: |
Línea 16: |
| | Si separamos las tres componentes del movimiento | | Si separamos las tres componentes del movimiento |
| | | | |
| - | <center><math>\vec{r}:\left\{\begin{array}{rcl} x & = &4A\cos(\Omega t) \\ y & = & 5A\,\mathrm{sen}(\Omega t)\\ z & = & 3A\cos(\Omega t)\end{array}\right.</math></center> | + | <center><math>\vec{r}=\begin{cases} x & = 4B\cos(\Omega t) \\ y & = 5B\,\mathrm{sen}(\Omega t}\\ z & = 3B\cos(\Omega t)\end{cases}</math></center> |
| - | | + | |
| - | De aquí es evidente que
| + | |
| - | | + | |
| - | <center><math>z = \frac{3}{4}x\qquad\Rightarrow\qquad 3x-4z =0</math></center>
| + | |
| - | | + | |
| - | Esta es la ecuación de un plano. También la podemos escribir en forma vectorial como
| + | |
| - | | + | |
| - | <center><math>\vec{n}\cdot\vec{r}=0</math></center>
| + | |
| - | | + | |
| - | ya que el vector de posición es
| + | |
| - | | + | |
| - | <center><math>\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}</math></center>
| + | |
| - | | + | |
| - | Si escribimos
| + | |
| - | | + | |
| - | <center><math>\vec{n} = a\vec{\imath}+b\vec{\jmath}+c\vec{k}</math></center>
| + | |
| - | | + | |
| - | El producto escalar es
| + | |
| - | | + | |
| - | <center><math>\vec{n}\cdot\vec{r} = ax + by +cz = 0</math></center>
| + | |
| - | | + | |
| - | Igualando coeficiente a coeficiente
| + | |
| - | | + | |
| - | <center><math>a = 3,\qquad b = 0,\qquad c = -4</math></center>
| + | |
| - | | + | |
| - | así que un vector normal al plano es
| + | |
| - | | + | |
| - | <center><math>\vec{n}=3\vec{\imath}-4\vec{k}</math></center>
| + | |
| - | | + | |
| - | que es un vector constante. Si queremos un unitario perpendicular al plano
| + | |
| - | | + | |
| - | <center><math>|\vec{n}|=\sqrt{3^2+4^2} = 5</math></center>
| + | |
| - | | + | |
| - | y queda
| + | |
| - | | + | |
| - | <center><math> \vec{B}=\frac{\vec{n}}{|\vec{n}|}=\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{k}</math></center>
| + | |
| - | | + | |
| - | El vector <math>\vec{B}</math> es un vector constante ortogonal al plano de movimiento.
| + | |
| - | | + | |
| - | Además tenemos que se cumple
| + | |
| - | | + | |
| - | <center><math>x^2 + z^2 = 25A^2\cos^2(\Omega t)\qquad\qquad y^2 = 25A^2\mathrm{sen}^2(\Omega t)</math></center>
| + | |
| - | | + | |
| - | y sumando estas dos
| + | |
| - | | + | |
| - | <center><math>x^2 + y^2 + z^2 = 25A^2\,</math></center>
| + | |
| - | | + | |
| - | que es la ecuación de una esfera de radio <math>R=5A</math>.
| + | |
| - | | + | |
| - | la trayectoria es entonces la intersección de un plano y una esfera. Esa intersección es siempre una circunferencia. Por tanto el movimiento es circular.
| + | |
| - | | + | |
| - | <center>[[Archivo:corte-plano-esfea.png]]</center>
| + | |
| - | | + | |
| - | ===Procedimiento cinemático===
| + | |
| - | El método anterior es muy simple para determinar que el movimiento es plano, pero no siempre se encuentra a la primera qué combinación lineal de las variables nos da la ecuación del plano, si este existe.
| + | |
| - | | + | |
| - | Por ello, existen procedimiento sistemáticos para determinar esta situación.
| + | |
| - | | + | |
| - | Uno es el siguiente: hay que hallar la velocidad, la aceleración y la derivada de ésta respecto al tiempo. El movimiento es plano si y solo si se cumple la condición
| + | |
| - | | + | |
| - | <center><math>(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}=0</math></center>
| + | |
| - | | + | |
| - | En nuestro caso tenemos
| + | |
| - | | + | |
| - | <center><math>\begin{array}{ccccccc}
| + | |
| - | \vec{v}(t) & = & -4A\Omega\,\mathrm{sen}(\Omega t)\vec{\imath}& + & 5A\Omega\,\mathrm{cos}(\Omega t)\vec{\jmath}& - & 3A\Omega\,\mathrm{sen}(\Omega t)\vec{k}\\
| + | |
| - | \vec{a}(t)& = & -4A\Omega^2\,\mathrm{cos}(\Omega t)\vec{\imath}& - & 5A\Omega^2\,\mathrm{sen}(\Omega t)\vec{\jmath}& - & 3A\Omega^2\,\mathrm{cos}(\Omega t)\vec{k}\\
| + | |
| - | \dot{\vec{a}}(t) & = & +4A\Omega^3\,\mathrm{sen}(\Omega t)\vec{\imath}& - &5A\Omega^3\,\mathrm{cos}(\Omega t)\vec{\jmath}& + & 3A\Omega^3\,\mathrm{sen}(\Omega t)\vec{k}\end{array}
| + | |
| - | </math></center>
| + | |
| - | | + | |
| - | El producto vectorial de la velocidad y la aceleración lo da el el determinante
| + | |
| - | | + | |
| - | <center><math>\vec{v}\times\vec{a}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -4A\Omega\,\mathrm{sen}(\Omega t) & 5A\Omega\,\mathrm{cos}(\Omega t)& - 3A\Omega\,\mathrm{sen}(\Omega t)\\
| + | |
| - | -4A\Omega^2\,\mathrm{cos}(\Omega t)& -5A\Omega^2\,\mathrm{sen}(\Omega t)& -3A\Omega^2\,\mathrm{cos}(\Omega t)\end{matrix}\right|=-15A^2\Omega^3\vec{\imath}+20A^2\Omega^3\vec{k}</math></center>
| + | |
| - | | + | |
| - | Siendo el producto mixto de los tres vectores
| + | |
| - | | + | |
| - | <center><math>(\vec{v}\times\vec{a})\cdot\dot{\vec{a}}=
| + | |
| - | -15A^2\Omega^3\left(4A\Omega^3\,\mathrm{sen}(\Omega t)\right)+20A^2\Omega^3\left(3A\Omega^3\,\mathrm{sen}(\Omega t)\right)=0</math></center>
| + | |
| - | | + | |
| - | Con eso ya tenemos que la trayectoria es plana. Para ver que además es circular vamos a calcular el radio de curvatura, según la fórmula
| + | |
| - | | + | |
| - | <center><math>R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}</math></center>
| + | |
| - | | + | |
| - | La rapidez del movimiento vale
| + | |
| - | | + | |
| - | <center><math>|\vec{v}|=\sqrt{16A^2\Omega^2\mathrm{sen}^2(\Omega t)+25A^2\Omega^2\mathrm{cos}^2(\Omega t)+9A^2\Omega^2\mathrm{sen}^2(\Omega t)}=5A\Omega</math></center>
| + | |
| - | | + | |
| - | Esta cantidad es constante por lo que ya sabemos además que el movimiento es uniforme.
| + | |
| - | | + | |
| - | Hallamos ahora el radio de curvatura
| + | |
| - | | + | |
| - | <center><math>R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}=\frac{(5A\Omega)^3}{A^2\Omega^3\sqrt{15^2+20^2}}=5A</math></center>
| + | |
| - | | + | |
| - | El radio de curvatura es constante.
| + | |
| - | | + | |
| - | Si el movimiento es plano y el radio de curvatura es constante, se trata de un movimiento circular.
| + | |
| - | | + | |
| - | ==Desplazamiento y distancia==
| + | |
| - | ===Desplazamiento===
| + | |
| - | Lo da la diferencia entre la posición final y la inicial
| + | |
| - | | + | |
| - | <center><math>\Delta\vec{r}=\vec{r}_f-\vec{r}_i</math></center>
| + | |
| - | | + | |
| - | Siendo la posición inicial
| + | |
| - | | + | |
| - | <center><math>\vec{r}_i=\vec{r}(t=0)=4A\cdot 1\vec{\imath}+5A\cdot0\vec{\jmath}+3A\cdot 1\vec{k}=4A\vec{\imath}+3A\vec{k}</math></center>
| + | |
| - | | + | |
| - | y la final la correspondiente a <math>\Omega t = \pi</math>
| + | |
| - | | + | |
| - | <center><math>\vec{r}_f=\vec{r}(t=\pi/\Omega)=4A\cdot(- 1)\vec{\imath}+5A\cdot0\vec{\jmath}+3A\cdot(- 1)\vec{k}=-4A\vec{\imath}-3A\vec{k}</math></center>
| + | |
| - | | + | |
| - | El desplazamiento vale entonces
| + | |
| - | | + | |
| - | <center><math>\Delta \vec{r}=-8A\vec{\imath}-6A\vec{k}</math></center>
| + | |
| - | | + | |
| - | El valor absoluto de este desplzamiento es la distancia en línea recta entre los dos puntos
| + | |
| - | | + | |
| - | <center><math>|\Delta\vec{r}| = \sqrt{64A^2+36A^2}=10A</math></center>
| + | |
| - | | + | |
| - | ===Distancia===
| + | |
| - | La calculamos integrando la rapidez
| + | |
| - | | + | |
| - | <center><math>\Delta s = \int_0^{\pi/\Omega} |\vec{v}|\mathrm{d}t = \int_0^{\pi/\Omega} 5A\Omega\,\mathrm{d}t = 5\pi A</math></center>
| + | |
| - | | + | |
| - | Esta distancia medida sobre la curva es mayor que la que se tiene en línea recta, que es la menor posible.
| + | |
| - | | + | |
| - | La interpretación es sencilla. Este movimiento es periódico. Cuando el argumento <math>\Omega t</math> varía en <math>2\pi</math> el seno y el coseno se repiten y la partícula vuelve a estar en la posición inicial. El tiempo que tarda en dar una vuelta completa es el periodo de revolución
| + | |
| - | | + | |
| - | <center><math>T=\frac{2\pi}{\Omega}</math></center>
| + | |
| - | | + | |
| - | Por tanto, el intervalo que estamos considerando es media vuelta. La distancia en línea recta es el diámetro de la circunferencia
| + | |
| - | | + | |
| - | <center><math>|\Delta\vec{r}| = 2R = 10A</math></center>
| + | |
| - | | + | |
| - | y la distancia sobre la curva es la longitud de media circunferencia
| + | |
| - | | + | |
| - | <center><math>\Delta s = \pi R = 5\pi A\,</math></center>
| + | |
| - | | + | |
| - | ==Tipo de movimiento==
| + | |
| - | En los apartados anteriores ya hemos establecido todo lo necesario para identificar el movimiento:
| + | |
| - | | + | |
| - | * Es plano
| + | |
| - | * Tiene radio de curvatura constante
| + | |
| - | * Tiene rapidez constante
| + | |
| - | | + | |
| - | Por tanto se trata de un movimiento circular uniforme.
| + | |
| - | | + | |
| - | ==Centro de la circunferencia==
| + | |
| - | El centro de la circunferencia coincide con el centro de curvatura
| + | |
| - | | + | |
| - | <center><math>\vec{r}_c = \vec{r}+R\vec{N}</math></center>
| + | |
| - | | + | |
| - | En este caso, al ser el movimiento uniforme la aceleración tangencial es nula y toda la aceleración es normal, por lo que
| + | |
| - | | + | |
| - | <center><math>\vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}=\frac{\vec{a}}{|\vec{a}|}=
| + | |
| - | \frac{ -4A\Omega^2\,\mathrm{cos}(\Omega t)\vec{\imath} - 5A\Omega^2\,\mathrm{sen}(\Omega t)\vec{\jmath} - 3A\Omega^2\,\mathrm{cos}(\Omega t)\vec{k}}{5A\Omega^2}=-\frac{4}{5}\,\mathrm{cos}(\Omega t)\vec{\imath} - \mathrm{sen}(\Omega t)\vec{\jmath} - \frac{3}{5}\,\mathrm{cos}(\Omega t)\vec{k}</math></center>
| + | |
| - | | + | |
| - | El radio de la circunferencia vale 5A, por lo que el centro se halla en
| + | |
| - | | + | |
| - | <center><math>\vec{r}_c = \left(4A\,\mathrm{cos}(\Omega t)\vec{\imath} +55A\,\mathrm{sen}(\Omega t)\vec{\jmath} +3A\,\mathrm{cos}(\Omega t)\vec{k}\right)+5A\left(-\frac{4}{5}\,\mathrm{cos}(\Omega t)\vec{\imath} - \mathrm{sen}(\Omega t)\vec{\jmath} - \frac{3}{5}\,\mathrm{cos}(\Omega t)\vec{k}\right)=\vec{0}</math></center>
| + | |
| - | | + | |
| - | Es decir, el centro de la circunferencia es el propio origen de coordenadas.
| + | |
| - | | + | |
| - | Esto se podía haber deducido de una forma más sencilla observando que cada coordenada es un seno o un coseno, por lo que la trayectoria es simétrica alrededor de <math>x=y=z=0</math> que es por tanto el centro de la circunferencia.
| + | |
| - | | + | |
| - | ==Cálculo de la velocidad angular==
| + | |
| - | Una vez que tenemos identificado el movimiento como circular podemos identificar la velocidad angular a partir de la ecuación
| + | |
| - | | + | |
| - | <center><math>\vec{v}=\vec{\omega}\times(\vec{r}-\vec{r}_c)</math></center>
| + | |
| - | | + | |
| - | La velocidad angular es un vector que tiene por dirección la del eje de la circunferencia, por sentido el dado por la regla de la mano derecha y por módulo el que resulta de
| + | |
| - | | + | |
| - | <center><math>|\vec{\omega}|=\frac{|\vec{v}|}{R}</math></center>
| + | |
| - | | + | |
| - | Existen varias formas de determinar este vector
| + | |
| - | | + | |
| - | ===A partir del módulo, dirección y sentido===
| + | |
| - | El módulo de esta velocidad angular cumple
| + | |
| - | | + | |
| - | <center><math>|\vec{\omega}|=\frac{|\vec{v}|}{R}=\frac{5\Omega A}{5A}=\Omega</math></center>
| + | |
| - | | + | |
| - | La dirección es la del eje. Este eje está en la dirección de la normal al plano de la circunferencia, dada por el vector unitario
| + | |
| - | | + | |
| - | <center><math>\vec{B}=\frac{3}{5}\vec{\imath}-\frac{4}{5}\vec{k}</math></center>
| + | |
| - | | + | |
| - | Por tanto
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}=\pm |\vec{\omega}|\vec{B}=\pm\left(\frac{3}{5}\Omega\vec{\imath}-\frac{4}{5}\Omega\vec{k}\right)</math></center>
| + | |
| - | | + | |
| - | La dualidad de signos no se debe a que tenga los dos valores al mismo tiempo, sino a que aun no tenemos claro el sentido de este vector, ya que la regla de la mano derecha no es inmediata de ver en 3D.
| + | |
| - | | + | |
| - | La forma más fácil de determinar el sentido es yendo directamente a la ecuación
| + | |
| - | | + | |
| - | <center><math>\vec{v}=\vec{\omega}\times\vec{r}</math></center>
| + | |
| - | | + | |
| - | donde ya hemos aplicado que sabemos que la partícula da vueltas alrededor del origen.
| + | |
| - | | + | |
| - | Desarrollando la expresión queda
| + | |
| - | | + | |
| - | <center><math> -4A\Omega\,\mathrm{sen}(\Omega t)\vec{\imath} + 5A\Omega\,\mathrm{cos}(\Omega t)\vec{\jmath} - 3A\Omega\,\mathrm{sen}(\Omega t)\vec{k}=\pm \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \displaystyle\frac{3}{5}\Omega & 0 & \displaystyle -\frac{4}{5}\Omega \\ 4A\Omega\,\mathrm{cos}(\Omega t) & 5A\Omega\,\mathrm{sen}(\Omega t) & 3A\Omega\,\mathrm{cos}(\Omega t)\end{matrix}\right|</math></center>
| + | |
| - | | + | |
| - | Desarrollando el determinante e igualando a la velocidad que aparece en el primer miembro se llega a que el signo correcto es el negativo y por tanto:
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}=-\frac{3}{5}\Omega\vec{\imath}+\frac{4}{5}\Omega\vec{k}</math></center>
| + | |
| - | | + | |
| - | ===Despejando de la velocidad===
| + | |
| - | Lo que parecería más sencillo sería despejar de la expresión
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}\times\vec{r}=\vec{v}</math></center>
| + | |
| - | | + | |
| - | Pero como sabemos, solo con el producto vectorial no tenemos información suficiente para hallar un vector y desde luego no podemos dividir por uno.
| + | |
| - | | + | |
| - | Tal como se ve en un problema de [[Determinaci%C3%B3n_de_un_vector_a_partir_de_sus_proyecciones|álgebra vectorial]], para poder hallar un vector <math>\vec{\omega}</math> necesitamos tanto su producto vectorial por uno conocido <math>\vec{r}</math> como su producto escalar.
| + | |
| - | | + | |
| - | Sin embargo, en este caso, sí conocemos este producto escalar. El vector de posición <math>\vec{r}</math> está en el plano de la circunferencia y <math>\vec{\omega}</math> es perpendicular a este plano, por lo que
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}\cdot\vec{r}=\vec{0}</math></center>
| + | |
| - | | + | |
| - | Por tanto sí tenemos los dos productos y podemos hallar la velocidad angular.
| + | |
| - | | + | |
| - | En la ecuación para la velocidad lineal multiplicamos vectorialmente por la posición
| + | |
| - | | + | |
| - | <center><math>\vec{r}\times(\vec{\omega}\times\vec{r})=\vec{r}\times\vec{v}</math></center>
| + | |
| - | | + | |
| - | Desarrollamos el doble producto vectorial
| + | |
| - | | + | |
| - | <center><math>\overbrace{(\vec{r}\cdot\vec{r})}^{=R^2}\vec{\omega}-\overbrace{(\vec{r}\cdot\vec{\omega})}^{=0}\vec{r}=R^2\vec{\omega}=\vec{r}\times\vec{v}</math></center>
| + | |
| - | | + | |
| - | y por tanto
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}=\frac{\vec{r}\times\vec{v}}{R^2}</math></center>
| + | |
| - | | + | |
| - | Sustituimos aquí las expresiones del radio, la posición y la velocidad
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}=\frac{1}{25A^2} \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 4A\Omega\,\mathrm{cos}(\Omega t) & 5A\Omega\,\mathrm{sen}(\Omega t) & 3A\Omega\,\mathrm{cos}(\Omega t) \\ -4A\Omega\,\mathrm{sen}(\Omega t) & 5A\Omega\,\mathrm{cos}(\Omega t) & - 3A\Omega\,\mathrm{sen}(\Omega t)\end{matrix}\right|</math></center>
| + | |
| - | | + | |
| - | Desarrollando el determinante se llega finalmente a que
| + | |
| - | | + | |
| - | <center><math>\vec{\omega}=-\frac{3}{5}\Omega\vec{\imath}+\frac{4}{5}\Omega\vec{k}</math></center>
| + | |
| - | | + | |
| | [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | | [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] |
con B y Ω constantes.
Podemos identificar la trayectoria a partir de razonamientos puramente geométricos o empleando procedimientos cinemáticos.