Estudio de un movimiento tridimensional

De Laplace

(Diferencias entre revisiones)

Revisión de 17:41 7 nov 2013

Contenido

1 Enunciado
2 Trayectoria
3 Ley horaria
4 Identificación del movimiento

1 Enunciado

Una partícula se mueve según las ecuaciones horarias

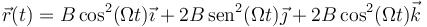
$\vec{r}(t)=B\cos^2(\Omega t)\vec{\imath}+2B\,\mathrm{sen}^2(\Omega t)\vec{\jmath}+2B\cos^2(\Omega t)\vec{k}$

¿Qué trayectoria sigue la partícula?
Determine la ley horaria $s (t)$ . Suponga que $s (0) = 0$ .
¿Qué tipo de movimiento describe la partícula?

2 Trayectoria

2.1 Método 1: Ecuaciones implícitas

La forma más directa de identificar la trayectoria consiste en buscar ecuaciones implícitas

$f(x,y,z) = 0\qquad\qquad g(x,y,z)=0$

que sean satisfechas por la posición instantánea en todo momento.

Separando en componentes tenemos que

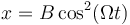
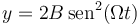
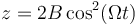
$x = B\cos^2(\Omega t)\,$ $y=2B\,\mathrm{sen}^2(\Omega t)$ $z=2B\cos^2(\Omega t)\,$

De aquí es inmediato que

$z= 2x\,$ $\Rightarrow$ $2x -z = 0\,$

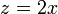
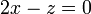
que es la ecuación de un plano, por lo que, por lo pronto, la trayectoria es plana.

Además, se verifica

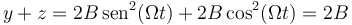
$y + z= 2B\,\mathrm{sen}^2(\Omega t)+ 2B\cos^2(\Omega t) = 2B$

con lo que la trayectoria está también contenida en el plano

$y + z= 2B\,$

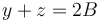
Al estar la trayectoria contenida en la intersección de dos planos, llegamos a la conclusión de que el movimiento es rectilíneo, siendo su trayectoria la recta

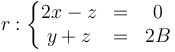
$r:\left\{\begin{matrix} 2x - z & = & 0 \\ y + z & = & 2B \end{matrix}\right.$

2.2 Método 2: Vector tangente

Un procedimiento sistemático para determinar si un movimiento es rectilíneo consiste en determinar el vector tangente a la trayectoria y ver si éste es constante.

Hallamos este vector tangente calculando previamente la velocidad

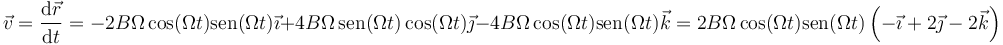
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-2B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)\vec{\imath}+4B\Omega\,\mathrm{sen}(\Omega t)\cos(\Omega t)\vec{\jmath}-4B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)\vec{k}=2B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)\left(-\vec{\imath}+2\vec{\jmath}-2\vec{k}\right)$

y dividiendo por su módulo, la celeridad,

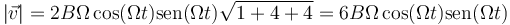
$|\vec{v}| = 2B\Omega \cos(\Omega t)\mathrm{sen}(\Omega t)\sqrt{1+4+4}=6B\Omega \cos(\Omega t)\mathrm{sen}(\Omega t)$

lo que nos da el vector tangente

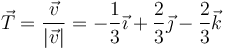
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{2}{3}\vec{k}$

Este vector es constante y por tanto el movimiento es rectilíneo. La ecuación de la recta la obtenemos a partir de la posición inicial y empleando este vector tangente como vector director

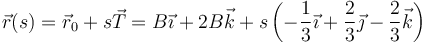
$\vec{r}(s) = \vec{r}_0 + s \vec{T} = B\vec{\imath}+2B\vec{k}+s\left(-\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{2}{3}\vec{k}\right)$

o, separando en componentes

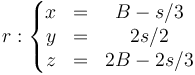
$r:\left\{\begin{matrix} x & = & B - s/3 \\ y & = & 2s/2 \\ z & = & 2B -2s/3\end{matrix}\right.$

2.3 Método 3: Relaciones trigonométricas

La trayectoria de la partícula también puede identificarse con ayuda de las relaciones trigonométricas

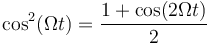
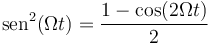
$\cos^2(\Omega t) = \frac{1+\cos(2\Omega t)}{2}$ $\mathrm{sen}^2(\Omega t) = \frac{1-\cos(2\Omega t)}{2}$

que permiten expresar la posición instantánea como

$\vec{r}(t)= \frac{B}{2}(1+\cos(2\Omega t))\vec{\imath}+B(1-\cos(2\Omega t))\vec{\jmath}+B(1+\cos(2\Omega t))\vec{k}$

Este vector se puede desglosar en la forma

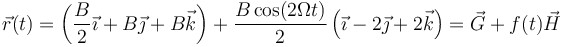
$\vec{r}(t) = \left(\frac{B}{2}\vec{\imath}+B\vec{\jmath}+B\vec{k}\right)+\frac{B\cos(2\Omega t)}{2}\left(\vec{\imath}-2\vec{\jmath}+2\vec{k}\right) = \vec{G}+f(t)\vec{H}$

siendo $\vec{G}$ y $\vec{H}$ dos vectores constantes. Dado que la dependencia con el tiempo queda solo en el coeficiente escalar de $\vec{H}$ , es claro que la trayectoria es rectilínea según la recta

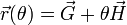
$\vec{r}(\theta) = \vec{G}+\theta\vec{H}$

3 Ley horaria

Para hallar la ley horaria, primero calculamos la velocidad, que ya vimos anteriormente,

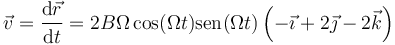
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=2B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)\left(-\vec{\imath}+2\vec{\jmath}-2\vec{k}\right)$

y hallamos su módulo, la celeridad,

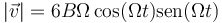
$|\vec{v}| = 6B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t)$

Esta cantidad es igual a la derivada del la distancia recorrida respecto al tiempo.

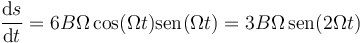
$\frac{\mathrm{d}s}{\mathrm{d}t}=6B\Omega\cos(\Omega t)\mathrm{sen}(\Omega t) = 3B\Omega\,\mathrm{sen}(2\Omega t)$

Calculamos la la ley horaria integrando esta expresión

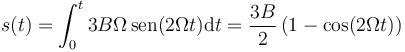
$s(t) = \int_0^t 3B\Omega\,\mathrm{sen}(2\Omega t)\mathrm{d}t=\frac{3B}{2}\left(1-\cos(2\Omega t)\right)$

En rigor, el módulo de la velocidad, que es una cantidad siempre positiva es solo igual a 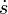$\dot{s}$ para $0 < 2Ω t < π$ , en la cual el seno es positivo. Podemos extender no obstante el resultado a cualquier valor de $t$ considerando que el valor del parámetro arco $s$ en cada punto de la trayectoria es igual al valor para este primer semiperiodo, y admitir que para el resto del tiempo, lo que hace la partícula es moverse adelante y atrás, aumentando y disminuyendo el valor de $s$ , pudiendo ser 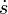$\dot{s}$ , la velocidad del movimiento rectilíneo, una cantidad tanto positiva como negativa.

4 Identificación del movimiento

Hemos determinado que el movimiento que sigue la partícula es rectilíneo, pero dentro de los movimientos rectilíneos existen muchas posibilidades. Puede ser uniforme, uniformemente acelerado, armónico simple, o no pertenecer a ningún tipo conocido.

Lo que marca el tipo de movimiento es la aceleración (nula para el uniforme, constante para el uniformemente acelerado, etc.), por lo que procedemos a calcular ésta. Derivando la velocidad

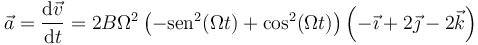
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}= 2B\Omega^2\left(-\mathrm{sen}^2(\Omega t)+\cos^2(\Omega t)\right)\left(-\vec{\imath}+2\vec{\jmath}-2\vec{k}\right)$

Esta aceleración no es constante, por lo que el movimiento no es ni uniforme ni uniformemente acelerado. Tampoco es evidente que se trate de un movimiento armónico simple, pero si observamos que

$\cos^2(\alpha)-\mathrm{sen}^2(\alpha) = 2\cos^2{\alpha}- 1 = 1 - 2\,\mathrm{sen}^2(\alpha)$

entonces podemos escribir la aceleración como

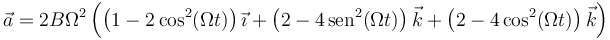
$\vec{a}=2B\Omega^2\left(\left(1-2\cos^2(\Omega t)\right)\vec{\imath}+\left(2-4\,\mathrm{sen}^2(\Omega t)\right)\vec{k}+\left(2-4\cos^2(\Omega t)\right)\vec{k}\right)$

Separando este vector en dos partes, equivale a

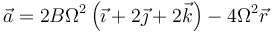
$\vec{a}= 2B\Omega^2\left(\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)-4\Omega^2\vec{r}$

o, lo que es lo mismo

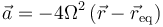
$\vec{a}=-4\Omega^2\left(\vec{r}-\vec{r}_\mathrm{eq}\right)$

donde

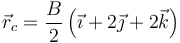
$\vec{r}_c = \frac{B}{2}\left(\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)$

Al escribirlo de esta forma vemos que la partícula cumple la ecuación del oscilador armónico

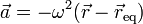
$\vec{a}=-\omega^2(\vec{r}-\vec{r}_\mathrm{eq})$

siendo en este caso la frecuencia angular

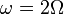
$\omega = 2\Omega\,$

Al cumplir la ecuación del oscilador armónico y ser el movimiento rectilíneo, se trata de un movimiento armónico simple.

Alternativamente, podemos dedducirlo de la propia ecuación horaria. Vectorialmente puede escribirse como

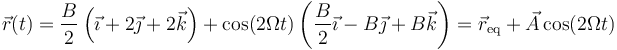
$\vec{r}(t) = \frac{B}{2}\left(\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)+\cos(2\Omega t)\left(\frac{B}{2}\vec{\imath}-B\vec{\jmath}+B\vec{k}\right)=\vec{r}_\mathrm{eq}+\vec{A}\cos(2\Omega t)$

que nos permite identificar el centro del movimiento como

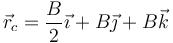
$\vec{r}_c = \frac{B}{2}\vec{\imath}+B\vec{\jmath}+B\vec{k}$

y la amplitud vectorial como

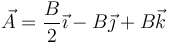
$\vec{A}=\frac{B}{2}\vec{\imath}-B\vec{\jmath}+B\vec{k}$

entendiendo que el módulo de este vector nos da la amplitud de las oscilaciones y su dirección nos da la dirección del movimiento oscilatorio.

@@ Línea 130: / Línea 130: @@
 donde
-<center><math>\vec{r}_c = \frac{B\Omega^2}{2}\left(\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)</math></center>
+<center><math>\vec{r}_c = \frac{B}{2}\left(\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)</math></center>
 Al escribirlo de esta forma vemos que la partícula cumple la ecuación del oscilador armónico

Estudio de un movimiento tridimensional

De Laplace

Revisión de 17:41 7 nov 2013

Contenido

1 Enunciado

2 Trayectoria

2.1 Método 1: Ecuaciones implícitas

2.2 Método 2: Vector tangente

2.3 Método 3: Relaciones trigonométricas

3 Ley horaria

4 Identificación del movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES