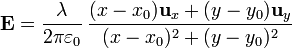Campo eléctrico de un segmento cargado

De Laplace

(Diferencias entre revisiones)

Revisión de 12:46 30 nov 2008

Contenido

1 Enunciado
2 Solución
- 2.1 Campo de un segmento cargado
- 2.2 Campo de un hilo infinito

1 Enunciado

Sea un segmento rectilíneo de longitud $L$ , sobre el cual existe una densidad de carga uniforme $λ$ .

Halle el campo eléctrico que produce en un punto arbitrario del espacio
1. ¿A qué se reduce el campo en el plano central del segmento?
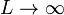
2. Calcule el límite del campo del segmento para $L\to\infty$
Halle el potencial que produce en un punto cualquiera del espacio.
Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.

2 Solución

2.1 Campo de un segmento cargado

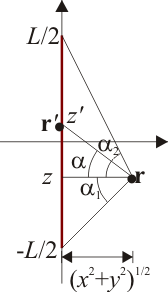
Sin pérdida de generalidad, podemos colocar el eje $z$ sobre el segmento y el origen de coordenadas en su punto medio.

La expresión integral para el campo eléctrico debido a una distribución de carga lineal se expresa

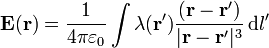
$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int\lambda(\mathbf{r}')\frac{(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}\,\mathrm{d}l'$

En nuestro caso, la posición de las fuentes es

$x'=0\quad y'=0\quad z'=z'$ $z'\in\left[-\frac{L}{2},\frac{L}{2}\right]$

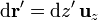
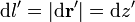
$\mathrm{d}\mathbf{r}'=\mathrm{d}z'\,\mathbf{u}_{z}$ $\mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=\mathrm{d}z'$

por lo que la integral se convierte en

$\mathbf{E}(\mathbf{r})=\frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2} \!\!\lambda \frac{(x\mathbf{u}_{x}+y\mathbf{u}_{y}+(z-z')\mathbf{u}_{z})} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$

Separando componente a componente

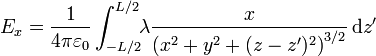
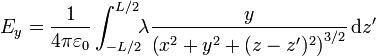
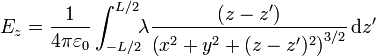
$E_x= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{ x} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$ $E_y= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{y} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$ $E_z= \frac{1}{4\pi\varepsilon_0} \int_{-L/2}^{L/2}\!\!\lambda \frac{ (z-z')} {\left(x^2+y^2+(z-z')^2\right)^{3/2}}\,\mathrm{d}z'$

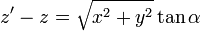
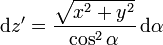
Podemos llevar a cabo estas integrales mediante el cambio de variable $z'-z=\sqrt{x^2+y^2}\tan\alpha$ $\mathrm{d}z'=\frac{\sqrt{x^2+y^2}}{\cos^2\alpha}\,\mathrm{d}\alpha$

Este ángulo posee interpretación geométrica ya que es el que forma la dirección al punto donde está la fuente con la horizontal.

Con este cambio las integrales quedan

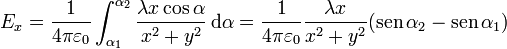
$E_x= \frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda x\cos\alpha} {x^2+y^2}\,\mathrm{d}\alpha=\frac{1}{4\pi\varepsilon_0} \frac{\lambda x}{x^2+y^2}(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1)$ $E_y= \frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda y\cos\alpha} {x^2+y^2}\,\mathrm{d}\alpha=\frac{1}{4\pi\varepsilon_0} \frac{\lambda y}{x^2+y^2}(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1)$ $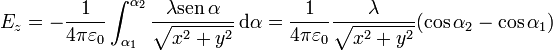E_z= -\frac{1}{4\pi\varepsilon_0} \int_{\alpha_1}^{\alpha_2}\frac{\lambda \mathrm{sen}\,\alpha} {\sqrt{x^2+y^2}}\,\mathrm{d}\alpha= \frac{1}{4\pi\varepsilon_0} \frac{\lambda }{\sqrt{x^2+y^2}}(\cos\alpha_2-\cos\alpha_1)$

Los senos y cosenos que aparecen en las expresiones anteriores corresponden a los valores límite de $α$ y su relación con las coordenadas cartesianas es

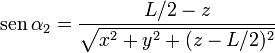
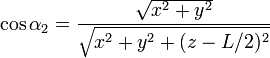
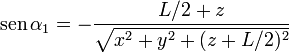
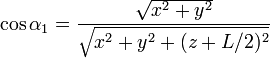
$\mathrm{sen}\,\alpha_2=\frac{L/2-z}{\sqrt{x^2+y^2+(z-L/2)^2}}$ $\cos\alpha_2=\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+(z-L/2)^2}}$ $\mathrm{sen}\,\alpha_1=-\frac{L/2+z}{\sqrt{x^2+y^2+(z+L/2)^2}}$ $\cos\alpha_1=\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+(z+L/2)^2}}$

Agrupando los resultados tenemos la forma vectorial

$\mathbf{E}=\frac{\lambda}{4\pi\varepsilon}\left(\frac{x\mathbf{u}_{x}+y\mathbf{u}_{y}}{x^2+y^2} \left(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1\right)+ \frac{\mathbf{u}_{z}(\cos\alpha_2-\cos\alpha_1)}{\sqrt{x^2+y^2}}\right)$

Si expresamos el campo en coordenadas cilíndricas centradas en el hilo nos queda

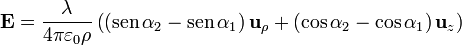
$\mathbf{E}=\frac{\lambda}{4\pi\varepsilon_0\rho} \left(\left(\mathrm{sen}\,\alpha_2-\mathrm{sen}\,\alpha_1\right)\mathbf{u}_{\rho}+ \left(\cos\alpha_2-\cos\alpha_1\right)\mathbf{u}_{z}\right)$

que podemos leer como el campo posee una componente en la dirección radial perpendicular al eje del segmento y una componente paralela a él. Esta interpretación nos seguirá valiendo cuando el eje $z$ no esté situado sobre el segmento.

Para ello consideraremos un segmento

A B

y un punto de observación arbitrario

P

. Trazamos la recta perpendicular a

A B

por

P

. Esta recta cortará a la primera en un punto

C

. La variable

ρ

será la longitud del segmento

P C

. El ángulo

α 1

será el que forma esta perpendicular con el segmento

P A

y el

α 2

con el segmento

P B

. Ambos ángulos serán positivos si la perpendicular queda por detrás del segmento (considerando adelante aquél en que apunta $\mathbf{u}_z$ ) y negativos en caso contrario. Si la perpendicular incide sobre el segmento

A B

, el ángulo

α 2

será positivo y el

α 1

negativo.

Este cálculo se puede hacer también numéricamente, de la forma que se muestra en este applet del Curso de Electricidad y Magnetismo del M.I.T. El resultado se puede ver en este otro applet.

2.2 Campo de un hilo infinito

Si tenemos un hilo infinitamente largo (que, obviamente, no existe en la realidad, pero sirve para modelar el campo de hilo muy largo como el de un cable de alta tensión si estamos a corta distancia de él), podemos hallar el campo que produce tomando el límite de la expresión anterior. Sea cual sea el punto de observación, 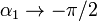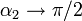$\alpha_1\to -\pi/2$ , $\alpha_2\to \pi/2$ , por lo que

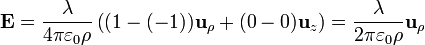
$\mathbf{E}=\frac{\lambda}{4\pi\varepsilon_0\rho}\left((1-(-1))\mathbf{u}_{\rho}+(0-0)\mathbf{u}_{z}\right)= \frac{\lambda}{2\pi\varepsilon_0\rho}\mathbf{u}_{\rho}$

Este resultado puede también obtenerse por aplicación de la ley de Gauss.

Lo que nos dice este resultado es que el campo producido por un hilo infinito es radial desde hilo y decae con la distancia como $1 / ρ$ (esto es, doble distancia, mitad de campo).

Si expresamos este campo en coordenadas cartesianas nos queda

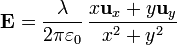
$\mathbf{E}= \frac{\lambda}{2\pi\varepsilon_0}\,\frac{x\mathbf{u}_x+y \mathbf{u}_y}{x^2+y^2}$

Si tenemos un hilo no situado en el eje $Z$ pero paralelamente a él, habrá que realizar la tralación de la expresión anterior. Así, si el hilo se encuentra sobre la vertical que pasa por $x = x 0$ , $y = y 0$ , la expresión correspondiente para el campo es

$\mathbf{E}= \frac{\lambda}{2\pi\varepsilon_0}\,\frac{(x-x_0)\mathbf{u}_x+(y-y_0) \mathbf{u}_y}{(x-x_0)^2+(y-y_0)^2}$

@@ Línea 2: / Línea 2: @@
 Sea un segmento rectilíneo de longitud <math>L</math>, sobre el cual existe una densidad de carga uniforme <math>\lambda</math>.
-* Halle el campo eléctrico que produce en un punto arbitrario del espacio
+# Halle el campo eléctrico que produce en un punto arbitrario del espacio
-** ¿A qué se reduce el campo en el plano central del segmento?
+## ¿A qué se reduce el campo en el plano central del segmento?
-** Calcule el límite del campo del segmento para <math>L\to\infty</math>
+## Calcule el límite del campo del segmento para <math>L\to\infty</math>
-* Halle el potencial que produce en un punto cualquiera del espacio.
+# Halle el potencial que produce en un punto cualquiera del espacio.
-* Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.
+# Demuestre que las equipotenciales son elipsoides con focos los extremos del segmento.
 ==Solución==

Campo eléctrico de un segmento cargado

De Laplace

Revisión de 12:46 30 nov 2008

Contenido

1 Enunciado

2 Solución

2.1 Campo de un segmento cargado

2.2 Campo de un hilo infinito

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES