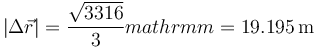Análisis de ecuación horaria
De Laplace
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | =Enunciado= | + | ==Enunciado== |
Una partícula se mueve por el espacio de forma que su posición, en las unidades fundamentales del SI, viene dada por la ecuación horaria | Una partícula se mueve por el espacio de forma que su posición, en las unidades fundamentales del SI, viene dada por la ecuación horaria | ||
| Línea 8: | Línea 8: | ||
# Calcule el radio de curvatura en t = 2 s así como el centro de curvatura en ese instante. | # Calcule el radio de curvatura en t = 2 s así como el centro de curvatura en ese instante. | ||
| - | =Desplazamiento y distancia= | + | ==Desplazamiento y distancia== |
| - | ==Desplazamiento== | + | ===Desplazamiento=== |
| + | El desplazamiento lo da la diferencia (vectorial) entre la posición final y la inicial | ||
| - | =Componentes intrínsecas de la aceleración= | + | <center><math>\Delta \vec{r}=\vec{r}(3\,\mathrm{s})-\vec{r}(1\,\mathrm{s})</math></center> |
| - | =Radio y centro de curvatura= | + | |
| + | Sustituyendo en la ecuación horaria | ||
| + | |||
| + | <center><math>\vec{r}(1\,\mathrm{s})=(\vec{\imath}+\vec{\jmath}+\frac{2}{3}\vec{k})\,\mathrm{m}\qquad\qquad \vec{r}(3\,\mathrm{s})=(9\vec{\imath}+3\vec{\jmath}+18\vec{k})\,\mathrm{m}</math></center> | ||
| + | |||
| + | resulta el desplazamiento | ||
| + | |||
| + | <center><math>\Delta \vec{r}=\left(7\vec{\imath}+2\vec{\jmath}+\frac{52}{3}\vec{k}\right)\mathrm{m}</math></center> | ||
| + | |||
| + | El módulo de este desplazamiento vale | ||
| + | |||
| + | <center><math>\left|\Delta\vec{r}\right|=\frac{\sqrt{3316}}{3}mathrm{m}=19.195\,\mathrm{m}</math></center> | ||
| + | ==Componentes intrínsecas de la aceleración== | ||
| + | ==Radio y centro de curvatura== | ||
[[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | ||
Revisión de 16:41 5 nov 2013
Contenido |
1 Enunciado
Una partícula se mueve por el espacio de forma que su posición, en las unidades fundamentales del SI, viene dada por la ecuación horaria

- Calcule el desplazamiento y la distancia que recorre la partícula entre t = 0 y t = 3 s.
- Halle las componentes intrínsecas de la aceleración en t = 2 s, como escalares y como vectores.
- Calcule el radio de curvatura en t = 2 s así como el centro de curvatura en ese instante.
2 Desplazamiento y distancia
2.1 Desplazamiento
El desplazamiento lo da la diferencia (vectorial) entre la posición final y la inicial

Sustituyendo en la ecuación horaria

resulta el desplazamiento
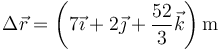
El módulo de este desplazamiento vale