Preguntas de test de herramientas matemáticas (GIE)
De Laplace
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | |||
==Suma de vectores ligados== | ==Suma de vectores ligados== | ||
Dados los vectores ligados de la figura, | Dados los vectores ligados de la figura, | ||
| Línea 21: | Línea 20: | ||
! D | ! D | ||
|} | |} | ||
| + | |||
| + | ===Solución=== | ||
| + | La respuesta correcta es la '''<span style="color:red;">C<span>'''. | ||
| + | |||
| + | Para que dos vectores ligados se puedan sumar, deben tener un punto de aplicación común. Como este no es el caso, estos vectores no se pueden sumar. | ||
==Ángulo entre dos vectores== | ==Ángulo entre dos vectores== | ||
| Línea 29: | Línea 33: | ||
* '''C''' 1.57 rad | * '''C''' 1.57 rad | ||
* '''D''' 2.07 rad | * '''D''' 2.07 rad | ||
| + | |||
| + | ==Solución== | ||
| + | Obtenemos el ángulo a partir del producto escalar de los dos vectores | ||
| + | |||
| + | <center><math>\vec{A}\cdot\vec{B}=|\vec{A}||\vec{B}|\cos(\alpha)\qquad\Rightarrow\qquad \alpha = \arccos\left(\frac{\vec{A}\cdot\vec{B}}{|\vec{A}||\vec{B}|}\right)</math></center> | ||
| + | |||
| + | Tenemos que | ||
| + | |||
| + | <center><math>\vec{A}\cdot\vec{B}=24\cdot 0+0\cdot 16+(-32)\cdot 12=-384</math></center> | ||
| + | |||
| + | y que | ||
| + | |||
| + | <center><math>|\vec{A}| = \sqrt{\vec{A}\cdot\vec{A}}=\sqrt{24^2+0^2+(-32)^2} = 40\qquad |\vec{B}| = \sqrt{\vec{B}\cdot\vec{B}}=\sqrt{0^2+16^2+12^2} = 20</math></center> | ||
| + | |||
| + | lo que nos da | ||
| + | |||
| + | <center><math>\cos(\alpha)=\frac{-384}{40\cdot20}=-\frac{12}{25}=-0.48\qquad\Rightarrow\qquad \alpha = 2.07\,\mathrm{rad}=118.7^\circ</math></center> | ||
==Posible igualdad vectorial== | ==Posible igualdad vectorial== | ||
Revisión de 07:58 27 oct 2013
Contenido |
1 Suma de vectores ligados
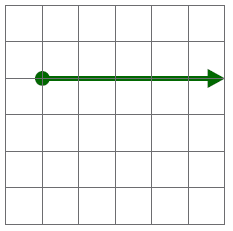
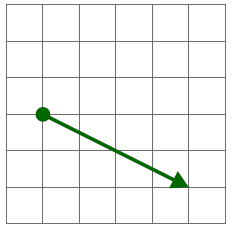
Dados los vectores ligados de la figura,
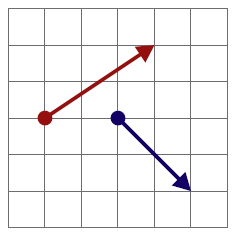
¿cuánto vale su suma vectorial?
| 
|
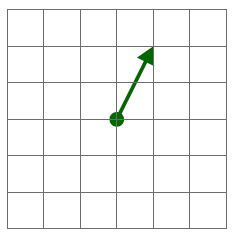
| A | B |
|---|---|
| 
|
| C | D |
1.1 Solución
La respuesta correcta es la C.
Para que dos vectores ligados se puedan sumar, deben tener un punto de aplicación común. Como este no es el caso, estos vectores no se pueden sumar.
2 Ángulo entre dos vectores
¿Qué ángulo forman los vectores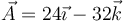 
y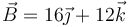 
?
- A 0.00 rad
- B 1.07 rad
- C 1.57 rad
- D 2.07 rad
3 Solución
Obtenemos el ángulo a partir del producto escalar de los dos vectores
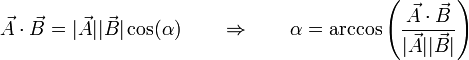
Tenemos que
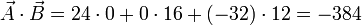
y que
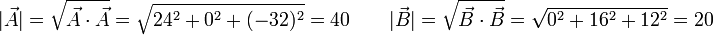
lo que nos da
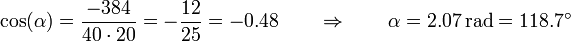
4 Posible igualdad vectorial
Si 
y 
son dos vectores unitarios, indique cuándo se cumple la igualdad
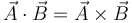
- A Cuando y son paralelos.
- B Cuando y son ortogonales.
- C No se cumple nunca.
- D Cuando y forman un ángulo de 45°.
5 Otra posible igualdad vectorial
Sean , y 
vectores arbitrarios no nulos. ¿Cuál de las siguientes afirmaciones es cierta siempre?
- A
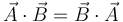
- B
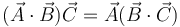
- C
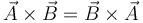
- D
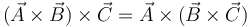
6 Área de un triángulo
Dados tres puntos del espacio A, B y C, siendo O el origen de coordenadas, ¿cómo podemos hallar el área del triángulo que definen?
- A
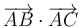
- B
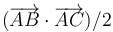
- C
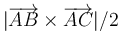
- D
