Dimensiones y unidades en el oscilador amortiguado

(Diferencias entre revisiones)

última version al 12:19 26 oct 2013

Un oscilador amortiguado obedece la ley de movimiento

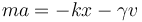
$ma = -kx -\gamma v\,$

¿Cuáles son las dimensiones de $k$ y $γ$ ? ¿Cuáles sus unidades en el SI?

Los tres términos que aparecen en la ecuación deben tener las mismas dimensiones

$[ma] = [kx] = [\gamma v]\,$

Sustituyendo las dimensiones de las cantidades conocidas

$M\frac{L}{T^2} = [k]L = [\gamma]\frac{L}{T}$

Despejando de aquí, tenemos para la constante k

$[k]= \frac{M}{T^2}$

y por tanto en el Si se medirá en

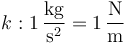
$k: 1\,\frac{\mathrm{kg}}{\mathrm{s}^2} =1 \,\frac{\mathrm{N}}{\mathrm{m}}$

mientras que $γ$ tiene dimensiones de

$[\gamma] = \frac{M}{T}$

y se mide en el SI en kg/s.

@@ Línea 22: / Línea 22: @@
 y por tanto en el Si se medirá en
-<center><math>k: 1\,\frac{\mathrm{kg}}{\mathrm{s}^2} = \,\frac{\mathrm{N}}{\mathrm{m}}</math></center>
+<center><math>k: 1\,\frac{\mathrm{kg}}{\mathrm{s}^2} =1 \,\frac{\mathrm{N}}{\mathrm{m}}</math></center>
 mientras que <math>\gamma</math> tiene dimensiones de