3.11. Partícula sujeta de dos hilos
De Laplace
(→Dos hilos) |
m (4.11. Partícula sujeta de dos hilos trasladada a 3.11. Partícula sujeta de dos hilos) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 38: | Línea 38: | ||
obtenemos la solución | obtenemos la solución | ||
| - | <center><math>\Phi_1 = \frac{5}{4}mg = | + | <center><math>\Phi_1 = \frac{5}{4}mg = 123\,\mathrm{N}</math>{{qquad}}{{qquad}} |
<math>\Phi_2 = \frac{3}{5}\Phi_1 = \frac{3}{4}mg = 74\,\mathrm{N}</math></center> | <math>\Phi_2 = \frac{3}{5}\Phi_1 = \frac{3}{4}mg = 74\,\mathrm{N}</math></center> | ||
Vemos que la tensión del primer hilo no ha disminuido por la colocación del segundo hilo, sino que ha aumentado en un 25%. | Vemos que la tensión del primer hilo no ha disminuido por la colocación del segundo hilo, sino que ha aumentado en un 25%. | ||
| - | [[Categoría:Problemas de dinámica del punto material (G.I.T.I.)]] | + | [[Categoría:Problemas de dinámica del punto material (G.I.T.I.)|8]] |
última version al 12:02 24 sep 2013
1 Enunciado
Una masa m = 10 kg cuelga inicialmente de un hilo de 50 cm de longitud sujeto del techo a una distancia de 80 cm de la pared más cercana. Para evitar que el primer hilo se rompa, se afianza la masa sujetándola con un hilo adicional de 50 cm atado horizontalmente a la pared. Determine la tensión de cada hilo. ¿Ha aumentado o disminuido la tensión del hilo original?
2 Un hilo
En el primer caso, la fuerza de reacción vincular, la tensión del hilo, es puramente vertical y debe compensar exactamente al peso
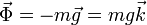
Sustituyendo los valores numéricos
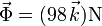
3 Dos hilos
En el segundo caso, tenemos dos incógnitas que son las dos tensiones de los hilos. Tenemos también dos ecuaciones, que son las dos componentes de la fuerza.
Al estar atado el segundo hilo horizontalmente y tener una longitud de 50 cm, esto quiere decir que el primer hilo queda inclinado, debiendo su extremo acercarse 30 cm a la pared. Puesto que su longitud es también de 50 cm, ello implica que su extremo inferior queda
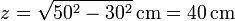
del techo. El ángulo que forma con la vertical, θ es tal que

El balance de fuerzas es ahora
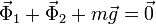
Separando en las componentes cartesianas
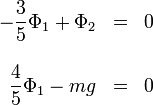
obtenemos la solución
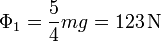
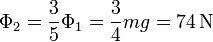
Vemos que la tensión del primer hilo no ha disminuido por la colocación del segundo hilo, sino que ha aumentado en un 25%.





