Inducción en espira cuadrada
De Laplace
(→Corriente inducida) |
|||
| Línea 49: | Línea 49: | ||
donde la resistencia del cable vale | donde la resistencia del cable vale | ||
| - | <center><math>R = \frac{l}{\sigma A}=\frac{2.0\,\mathrm{m}}{5.96\times 10^7\mathrm{S}/\mathrm{m}\pi(10^-4/2)^2\mathrm{m}^2}=4.27\,\Omega</math></center> | + | <center><math>R = \frac{l}{\sigma A}=\frac{2.0\,\mathrm{m}}{5.96\times 10^7\mathrm{S}/\mathrm{m}\pi(10^{-4}/2)^2\mathrm{m}^2}=4.27\,\Omega</math></center> |
| + | |||
| + | por lo que resulta la corriente | ||
| + | |||
| + | <center><math>I = 1.84\mathrm{sen}(100\pi t)\,\mathrm{A}</math></center> | ||
| + | |||
| + | La corriente es sinusoidal, como la fuerza electromotriz. Lo que estamos describiendo es un sencillo generador de corriente alterna. | ||
| + | |||
==Potencia disipada== | ==Potencia disipada== | ||
==Energía disipada== | ==Energía disipada== | ||
Revisión de 19:53 17 sep 2013
Contenido |
1 Enunciado
Con 2 m de un fino cable de cobre (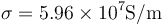
) de sección circular de 0.10 mm de diámetro se construye una espira de forma cuadrada. Esta espira se coloca perpendicularmente a un campo magnético
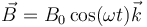
con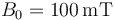 
y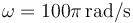 
.
- Calcule la fuerza electromotriz inducida como función del tiempo.
- Halle la corriente que circula por la espira como función del tiempo.
- Determine la potencia disipada por efecto Joule en el hilo como función del tiempo.
- Calcule la energía total disipada por efecto Joule a largo de un periodo de oscilación del campo magnético.
Despréciese la autoinducción de la espira.
2 Fuerza electromotriz
De acuerdo con la ley de Faraday, la fuerza electromotriz inducida en la espira vale
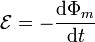
siendo Φm el flujo magnético a través de una superficie apoyada en la espira.
En nuestro caso, esta superficie es un cuadrado de lado 2m/4 = 0.5 m, que tiene un área
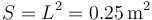
y consideramos un sentido de recorrido antihorario alrededor del eje OZ, de forma que el vector normal a la superficie es 
El flujo del campo magnético se calcula mediante la integral
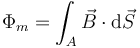
puesto que el campo magnético es independiente de la posición (solo depende del tiempo) y es paralelo al vector superficie, por lo que la integral se reduce a una multiplicación
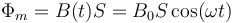
Derivando esta expresión respecto al tiempo hallamos la f.e.m.
Numéricamente
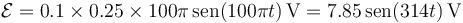
3 Corriente inducida
Una vez que tenemos la f.e.m. hallamos la corriente aplicando la ley de Ohm
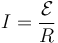
donde la resistencia del cable vale
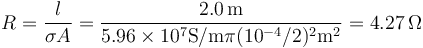
por lo que resulta la corriente
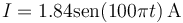
La corriente es sinusoidal, como la fuerza electromotriz. Lo que estamos describiendo es un sencillo generador de corriente alterna.
