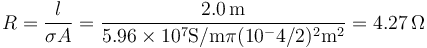Inducción en espira cuadrada
De Laplace
(→Fuerza electromotriz) |
|||
| Línea 43: | Línea 43: | ||
==Corriente inducida== | ==Corriente inducida== | ||
| + | Una vez que tenemos la f.e.m. hallamos la corriente aplicando la ley de Ohm | ||
| + | |||
| + | <center><math>I=\frac{\mathcal{E}}{R}</math></center> | ||
| + | |||
| + | donde la resistencia del cable vale | ||
| + | |||
| + | <center><math>R = \frac{l}{\sigma A}=\frac{2.0\,\mathrm{m}}{5.96\times 10^7\mathrm{S}/\mathrm{m}\pi(10^-4/2)^2\mathrm{m}^2}=4.27\,\Omega</math></center> | ||
==Potencia disipada== | ==Potencia disipada== | ||
==Energía disipada== | ==Energía disipada== | ||
Revisión de 19:51 17 sep 2013
Contenido |
1 Enunciado
Con 2 m de un fino cable de cobre (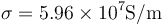
) de sección circular de 0.10 mm de diámetro se construye una espira de forma cuadrada. Esta espira se coloca perpendicularmente a un campo magnético
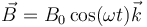
con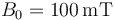 
y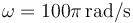 
.
- Calcule la fuerza electromotriz inducida como función del tiempo.
- Halle la corriente que circula por la espira como función del tiempo.
- Determine la potencia disipada por efecto Joule en el hilo como función del tiempo.
- Calcule la energía total disipada por efecto Joule a largo de un periodo de oscilación del campo magnético.
Despréciese la autoinducción de la espira.
2 Fuerza electromotriz
De acuerdo con la ley de Faraday, la fuerza electromotriz inducida en la espira vale
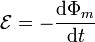
siendo Φm el flujo magnético a través de una superficie apoyada en la espira.
En nuestro caso, esta superficie es un cuadrado de lado 2m/4 = 0.5 m, que tiene un área
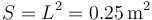
y consideramos un sentido de recorrido antihorario alrededor del eje OZ, de forma que el vector normal a la superficie es 
El flujo del campo magnético se calcula mediante la integral
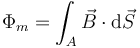
puesto que el campo magnético es independiente de la posición (solo depende del tiempo) y es paralelo al vector superficie, por lo que la integral se reduce a una multiplicación
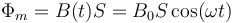
Derivando esta expresión respecto al tiempo hallamos la f.e.m.
Numéricamente
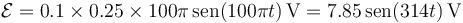
3 Corriente inducida
Una vez que tenemos la f.e.m. hallamos la corriente aplicando la ley de Ohm
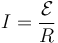
donde la resistencia del cable vale
