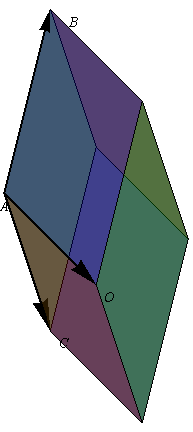
1.10. Volumen de un paralelepípedo
De Laplace
m (2.10. Volumen de un paralelepípedo trasladada a 1.10. Volumen de un paralelepípedo) |
|||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 61: | Línea 61: | ||
y que el producto vectorial de <math>\overrightarrow{OA}</math> por cualquier cosa es ortogonal a <math>\overrightarrow{OA}</math> llegamos a | y que el producto vectorial de <math>\overrightarrow{OA}</math> por cualquier cosa es ortogonal a <math>\overrightarrow{OA}</math> llegamos a | ||
| - | <center><math>\left(\overrightarrow{OA}\times\overrightarrow{OB})\cdot\left(\overrightarrow{OC}-\overrightarrow{OA}\right) = \left(\overrightarrow{OA}\times\overrightarrow{OB})\cdot\overrightarrow{OC}</math></center> | + | <center><math>\left(\overrightarrow{OA}\times\overrightarrow{OB}\right)\cdot\left(\overrightarrow{OC}-\overrightarrow{OA}\right) = \left(\overrightarrow{OA}\times\overrightarrow{OB}\right)\cdot\overrightarrow{OC}</math></center> |
Concluimos entonces que | Concluimos entonces que | ||
| Línea 68: | Línea 68: | ||
==Volumen del tetraedro== | ==Volumen del tetraedro== | ||
| - | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | + | [[Archivo:volumen-paralelepipedo-03.png|right]] |
| + | |||
| + | Un tetraedro es un caso particular de pirámide. El volumen de una pirámide es 1/3 del volumen del prisma que tiene la misma base y la misma altura. Si tomamos como base el triángulo definido por O, A y B, la altura es la proyección de <math>\overrightarrow{OC}</math> en la dirección normal a la superficie | ||
| + | |||
| + | <center><math>V_t = \frac{1}{3}\left|\vec{S}\cdot\overrightarrow{OC}\right|</math></center> | ||
| + | |||
| + | El área de un triángulo es área es 1/2 del área del paralelogramo definido por dos de sus lados. | ||
| + | |||
| + | <center><math>\vec{S}=\frac{1}{2}\overrightarrow{OA}\times\overrightarrow{OB}</math></center> | ||
| + | |||
| + | Por tanto, el volumen del tetraedro es (1/3)×(1/2) = 1/6 del volumen del paralelepípedo definido por tres aristas concurrentes del tetraedro, esto es | ||
| + | |||
| + | <center><math>V_t = \frac{1}{6}\left|(\overrightarrow{OA}\times\overrightarrow{OB})\cdot\overrightarrow{OC}\right| = \frac{10}{3}\,\mathrm{m}^3</math></center> | ||
| + | |||
| + | Puesto que podemos elegir cualquier vértice del tetraedro para tomar las tres aristas concurrentes, y el volumen de un paralelepípedo es siempre 6 veces el del tetraedro, llegamos de forma inmediata a la afirmación anterior de que todos los paralelepípedos definidos por los mismos cuatro puntos tienen el mismo volumen. | ||
| + | |||
| + | [[Categoría:Problemas de vectores libres (G.I.T.I.)|6]] | ||
última version al 18:45 13 sep 2013
Contenido |
1 Enunciado
Sean los puntos de coordenadas (en el SI) O(1,0,2), A(3,2,4), B(2,6,8) y C(2, − 3,1). Determine el volumen del paralelepípedo definido por los vectores  ,
, 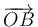 y
y  .
.
Halle del mismo modo el volumen del paralelepípedo definido por los vectores  ,
, 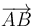 y
y 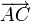 .
.
Calcule igualmente el volumen del tetraedro irregular definido por estos cuatro puntos.
2 Primer volumen
El volumen de un paralelepípedo se calcula como el producto mixto (sin signo) de los tres vectores que definen el paralelepíedo.
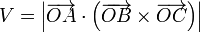
En nuestro caso los vectores los obtenemos hallando las diferencias entre las coordenadas de cada par de puntos
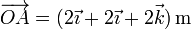
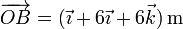
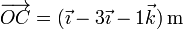
de forma que el producto mixto lo da el determinante
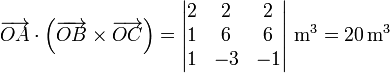
Al ser positivo, este es el volumen del paralelepípedo.
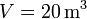
3 Segundo volumen
Para el segundo paralelepípedo calculamos los nuevos vectores de posición relativos
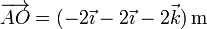
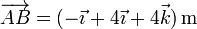
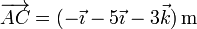
El nuevo producto mixto es
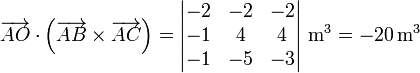
Puesto que el volumen debe ser positivo obtenemos
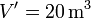
Este es el mismo resultado que antes, pese a que geométricamente estemos hablando de un paralelepípedo diferente. Puede demostrarse en general: un paralelepípedo definido por cuatro puntos a partir de tres vectores concurrentes que unen uno de los puntos con los otros tres posee el mismo volumen sea cual sea el punto de los cuatro que tomemos como origen de los vectores.
Para este caso la demostración parte de
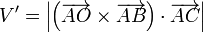
aplicando que
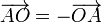
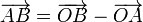
nos queda, para el primer producto vectorial

ya que el producto vectorial de un vector por si mismo es nulo. Aplicando ahora que
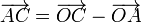
y que el producto vectorial de  por cualquier cosa es ortogonal a
por cualquier cosa es ortogonal a  llegamos a
llegamos a
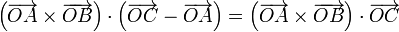
Concluimos entonces que
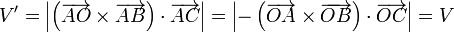
4 Volumen del tetraedro
Un tetraedro es un caso particular de pirámide. El volumen de una pirámide es 1/3 del volumen del prisma que tiene la misma base y la misma altura. Si tomamos como base el triángulo definido por O, A y B, la altura es la proyección de  en la dirección normal a la superficie
en la dirección normal a la superficie
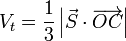
El área de un triángulo es área es 1/2 del área del paralelogramo definido por dos de sus lados.
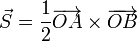
Por tanto, el volumen del tetraedro es (1/3)×(1/2) = 1/6 del volumen del paralelepípedo definido por tres aristas concurrentes del tetraedro, esto es
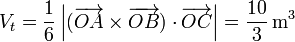
Puesto que podemos elegir cualquier vértice del tetraedro para tomar las tres aristas concurrentes, y el volumen de un paralelepípedo es siempre 6 veces el del tetraedro, llegamos de forma inmediata a la afirmación anterior de que todos los paralelepípedos definidos por los mismos cuatro puntos tienen el mismo volumen.